「データ解析のための統計モデリング入門」の著者の久保拓弥氏へのお返事なのですが、別所の「統計モデルに観測値と観測値の割り算値を入れても問題ない」に対して以下のようなコメントをもらったので、具体的な例を作ってみました*1。
…まあ,みなさん割算値だい好きだし,これからも割算値いりの統計モデルが使われるのでしょう.とりあえず「この場合は明らかにかなりまずいでしょ」とわかる例を何か作ってみようかな…
誤差項がコーシー分布のようなものになったときに、どのぐらいバイアスがかかるのかに関して、直観的な話です。
1. 真のモデルに割り算が無いケースを考える
以下のようなx、y、zの関係を現す真のモデルを考えます。
「観測値は非確率変数で、未知の何かが誤差項を作っている」と仮定すると終了するので、xの観測値x'はxと正規分布に従う観測誤差、yの観測値y'はと正規分布に従う観測誤差の合算とします。後のシミュレーションでパラメーターを減らすために、xとyの観測誤差はi.i.dとします。
変形してみましょう。
単純に推定すると1/yの影響を忘れてかなり大きな誤差が出ます。x/yがモデルに入るときは、1/yの影響が無い事が理論的に演繹されている気もしますが、今回は特定化バイアスではなく誤差の分布の影響を比較するために残します。
推定モデルを整理しておきます。εとηは誤差項です。
割り算なし:
割り算あり:
一様分布からxとyを作り出しzを計算して、xとyに誤差項を加えてx'とy'を作ってから、x'、y'、zでデータセットを作成し、そこからの推定量を計算していきます。真の値は2です。
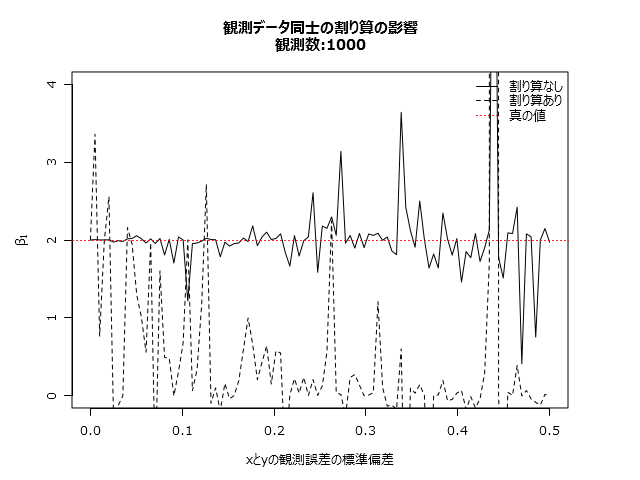
さて、割り算なしと割り算ありの違いを見てみましょう。
観測値の誤差が小さい場合は差は目立ちませんが、誤差が大きくなると割り算ありモデルの推定結果が不安定になります。「この場合は明らかにかなりまずいでしょ」とわかる例に思えるかも知れませんが、実は説明力を失って、真の値から乖離している領域であることに注意してください。なお測定誤差が大きくなると、切片項以外の推定される係数はゼロに近づきます。
なお割り算ありモデルの残差にシャピロ-ウィルク検定をかけると、ほぼ正規分布にならない事が分かります。一方で、割り算なしモデルの残差はほとんど正規分布していました。無理に割り算を入れるのは、よした方が良いようです。
2. 真のモデルに割り算があるケースを考える
以下のようなx、y、zの関係を現す真のモデルを考えます。
xとyの観測値の誤差は正規分布だと考えるので、x/yの観測誤差の分布はコーシー分布になります。
推定モデルを整理しておきます。
割り算なし:
割り算あり:
これも「この場合は明らかにかなりまずいでしょ」とわかる例に思えるかも知れませんが、ある程度は信頼のおける推定値である青点線の左側では、割り算のありなしで大差は見られません。
なお、こちらの推定の残差にシャピロ-ウィルク検定をかけると、どちらもほとんど正規分布ではないことになります。割り算ありモデルは割り算で、割り算なしモデルは掛け算で分布が歪んでしまうようです。
2.1 本当にヤバいぐらい壊れるケース
後から気づいたので追記します。setup関数内のxとyの初期値を以下にして、第2節のグラフを描くと以下のように割り算で派手に壊れます。
x <- rnorm(n, sd=5) # xの真の値(0にかかる正規分布)
y <- rnorm(n, sd=5) # yの真の値(0にかかる正規分布)
何が起きたのかと思っていたのですが、偶発的に異常値がx/yにできるので、それに推定結果が引っ張られてしまったようです。以下がループ中で推定値が飛んだとき(setupの引数がsd=0.03)のヒストグラム。
(;゚д゚) -200以下と、+100以上!?
xとyの真の値の分布がrnorm(n, sd=5) + 30だったりすると問題が出ないので、常に問題になるわけではないですが、x/yの分布図は見ておいたほうが無難みたいです。
3. モデルの特定化の方が大事に思える
誤差の大きさや特定化の精度の程度によりますが、割り算による影響が大きいとは限りません。どこかの演習問題でx/yの誤差の分布は正規分布で近似できるとありましたが、ある程度はそういう性質があるようです。
少なくとも観測値が非確率的と見なせるほど精度が高ければ気にしなくて良いですし、質的選択モデルのような計量モデルの都合で割り算を排除できないときに、観測値と観測値の割り算をためらう理由も無い気がします。心配性の人は、残差の分布を確認しましょう。
割り算を排除したとしても、それによってモデルの特定化に失敗していたら、誤差は大きくなります。変数をかけたり*2、対数をとったりしても誤差の分布は歪むわけです。現実的に完璧な推定はあり得ませんから、力の入れどころは考えていく必要があると思います。
A. ソースコード
上のグラフ二枚のプロットに使ったコードは以下になります。
#
# n: 観測数, sd: 標準偏差, hg: 不均一分散(TRUE/FALSE)
# model: 真のモデルの数式表記
# return: x, y, zの観測値
#
setup <- function(n=100, sd=1, hg=FALSE, model=parse(text="1+2*x-3*y")){
x <- runif(n, 1, 3) # xの真の値
y <- runif(n, 1, 2) # yの真の値
u <- rnorm(n, sd=sd) # yの観測誤差
oy <- y + u # yの観測値
e <- rnorm(n, sd=sd) # xの観測誤差
# 不均一分散のときは上書き
if(hg){
for(i in 1:n){
e[i] <- rnorm(1, sd=max(1e-6, sd*y[i])) # 標準偏差は0より僅かに正にする
}
}
ox <- x + e # xの観測値
# 被説明変数zは真の値に従う
z <- eval(model)
data.frame(x = ox, y = oy, z=z)
}
#
# シミュレーションで比較してプロット
# n: 観測数, min_sd: 標準偏差の最小値, max_sd: 標準偏差の最大値
# hg: TRUEならば不均一分散を入れる(未使用)
# model: 真のモデルのテキスト表記
# plegend: 凡例の位置
#
compare <- function(n=100, min_sd=1e-06, max_sd=1, hg=FALSE, model="1+2*x-3*y", plegend="topright"){
len <- 100
compared <- data.frame(sd=numeric(len), non_divided=numeric(len), divided=numeric(len), nd_sw_test=numeric(len), d_sw_test=numeric(len), t_test=integer(len))
compared$sd <- seq(max(1e-06, min_sd), max_sd, length.out=len)
for(i in 1:len){
df <- setup(n=n, sd=compared$sd[i], hg=hg, model=parse(text=model))
# ベタベタな分岐
if(model=="1+2*x-3*y"){
# 普通に推定
r <- lm(z ~ x + y, data=df)
# 割り算推定
z_p_oy <- df$z/df$y
x_p_oy <- df$x/df$y
c_p_oy <- 1/df$y
r_p_oy <- lm(z_p_oy ~ x_p_oy + c_p_oy)
}else{
# 割り算あり
yz = df$z*df$y
r <- lm(yz ~ y + x + 0, data=df)
# 割り算なし
x_p_oy <- df$x/df$y
r_p_oy <- lm(df$z ~ x_p_oy)
}
# 切片項
compared$non_divided[i] <- coef(r)[2]
compared$divided[i] <- coef(r_p_oy)[2]
# 正規性の検定結果
compared$nd_sw_test[i] <- shapiro.test(residuals(r))$p.value
compared$d_sw_test[i] <- shapiro.test(residuals(r_p_oy))$p.value
# 95%信頼区間に2.0が含まれるか
compared$t_test[i] <- ifelse(abs(2.0 - coef(r)[2])<coef(summary(r))[, 2][2]*qt(1-0.05/2, r$df.residual), 1, 0)
}
# ylim <- c(min(compared$non_divided, compared$divided), max(compared$non_divided, compared$divided))
ylim <- c(0, 4)
plot(non_divided ~ sd, data=compared, xlim=c(min_sd, max_sd), ylim=ylim, type="l", main=sprintf("観測データ同士の割り算の影響\n観測数:%d%s", n, ifelse(hg,",不均一分散あり","")), xlab=sprintf("xとyの観測誤差の標準偏差%s", ifelse(hg, "(y=1のとき)", "")), ylab=parse(text = "beta[1]"))
lines(compared$sd, compared$divided, lty=2)
abline(h=2, col="red", lty=3)
# ある程度の信頼性の推定値を出した最大の標準偏差
rsd <- max(subset(compared, t_test==1)$sd)
abline(v=rsd, col="blue", lty=4)
text(rsd, 0, "推定値の95%信頼区間に2が入る限界線", col="blue", adj=c(0, 0))
legend(plegend, lty=c(1, 2, 3), pch=-1, legend=c("割り算なし", "割り算あり", "真の値"), col=c("black","black","red"), bty="n")
return(compared)
}
# 第1節のグラフ
set.seed(201408)
rd <- compare(max_sd=0.5, n=1000)
# 第2節のグラフ
set.seed(201408)
rd <- compare(max_sd=0.5, n=1000, model="1+2*(x/y)")
B. 不均一分散
こうすると不均一分散があるときに、割り算があるときのほうが、マシな推定量になる事が分かります。まぁ、クマが体長10cmから50mまであったりしないでしょうから、社会科学系のデータでないと気にする必要はないかも知れませんが。
set.seed(201408)
rd <- compare(max_sd=0.5, n=1000, hg=TRUE)


