餡子付゛録゛

ソフトウェア開発ツールの便利な使い方を紹介。

インストーラー作成ツールNSISをいじってみる

Windows

MS-Windowsのアプリケーションのためにインストーラーを作るときは、Microsoft Windows InstallerかInstallShieldが定番になっていると思いますが、Qtなどオープンソースで開発しているときはライセンス料の問題などで使いづらいかも知れません*1。しかし、そういう時は、フリーソフトのNSIS (Nullsoft Scriptable Install System)があるので、これを使えばいいようです。スクリプト・ファイルを使わないといけないので取っ付きづらい感じもあるのですが、試しに使ってみました。

1. 準備する

まずはNSISをこちらからダウンロードしてきます。数年前にダウンロードしてあったバージョン2.46と、最新版の3.0βで試しましたが、大した事をしなければ差異は無いようです。
次にWindows Applicationを用意します。ただのテキスト・ファイルでも問題ないのですが、昔書いた巡回セールスマン問題解法プログラムを引っ張り出してきます。

2. NSISをインストールする

ダウンロードしてきたnsis-2.46-setup.exeを実行します。インストーラーのメッセージは英語ですが、ライセンス条項に I agree をして、デフォルト構成でインストールして問題ないと思います。コマンド・プロンプトで makensis コマンドを使う事になりますが、C:\Program Files (x86)\NSIS などのインストール先にパスを通してくれないので注意しましょう。

3. スクリプトファイルを記述する

巡回セールスマン問題解法プログラムは、本体とドキュメントとQt関連のDLLのみで構成されたシンプルなものです。今回は、本体とドキュメントを%PROGRAMFILES%\TSP以下に置き、Qt関連のDLLをWindowsのシステム・ディレクトリに置くようにインストーラを書いてみました。

; ライブラリ操作を行うマクロを読み込む
!include "Library.nsh"


Name "TSP Installer" ; インストーラーの名前
OutFile "TSPInst.exe" ; インストーラーのファイル名


; インストール先ディレクトリ
InstallDir "$PROGRAMFILES\TSP"


; 必要な実行権限（user/admin）
RequestExecutionLevel admin


; インストール時に表示するものを指定
Page license ; ライセンスを表示（他のページより先に書く必要あり）
Page directory ; インストール先ディレクトリを表示
Page instfiles ; インストールしたファイル名を表示


; アンインストール時に表示するものを指定
UninstPage uninstConfirm ; アンインストールの確認
UninstPage instfiles ; アンインストールしたファイル名を表示


; 日英で国際化する。
LoadLanguageFile "${NSISDIR}\Contrib\Language files\English.nlf"
LoadLanguageFile "${NSISDIR}\Contrib\Language files\Japanese.nlf"


; ライセンス文書は日英別（rtfも使える）
LicenseLangString license ${LANG_ENGLISH} license-english.txt
LicenseLangString license ${LANG_JAPANESE} license-japanese.txt
LicenseData $(license)


; 日英でディレクトリ名を変える
LangString ShortcutDirectory ${LANG_ENGLISH} "Travelling Salesman Problem"
LangString ShortcutDirectory ${LANG_JAPANESE} "巡回セールスマン問題解法プログラム"


; インストール時の挙動
Section "Install" ; この名前は重要ではない


; インストール先ディレクトリを指定
SetOutPath $INSTDIR


; 変数定義
!define ReleaseDirectory 巡回セールスマン問題解法プログラム
!define RegistryKey "Software\Microsoft\Windows\CurrentVersion\Uninstall\TSP"


; インストールするファイルを指定
File ..\${ReleaseDirectory}\TSP.exe
File ..\${ReleaseDirectory}\readme.txt
File ..\${ReleaseDirectory}\TSP_ja_JP.qm


; 上書きインストールの場合は、DLLは展開しない
Var /GLOBAL ALREADY_INSTALLED
IfFileExists "$INSTDIR\TSP.exe" 0 new_installation
StrCpy $ALREADY_INSTALLED 1
new_installation:
; DLLをシステム・ディレクトリに展開
!insertmacro InstallLib DLL $ALREADY_INSTALLED REBOOT_NOTPROTECTED ..\${ReleaseDirectory}\QtCore4.dll $SYSDIR\QtCore4.dll $SYSDIR
!insertmacro InstallLib DLL $ALREADY_INSTALLED REBOOT_NOTPROTECTED ..\${ReleaseDirectory}\QtGui4.dll $SYSDIR\QtGui4.dll $SYSDIR
!insertmacro InstallLib DLL $ALREADY_INSTALLED REBOOT_NOTPROTECTED ..\${ReleaseDirectory}\libgcc_s_dw2-1.dll $SYSDIR\libgcc_s_dw2-1.dll $SYSDIR
!insertmacro InstallLib DLL $ALREADY_INSTALLED REBOOT_NOTPROTECTED ..\${ReleaseDirectory}\mingwm10.dll $SYSDIR\mingwm10.dll $SYSDIR


; アンインストーラーを書き出す
WriteUninstaller $INSTDIR\uninstaller.exe


; スタートメニューのショートカットを作る
CreateDirectory "$SMPROGRAMS\$(ShortcutDirectory)"
CreateShortCut "$SMPROGRAMS\$(ShortcutDirectory)\TSP.lnk" $INSTDIR\TSP.exe
CreateShortCut "$SMPROGRAMS\$(ShortcutDirectory)\uninstaller.lnk" $INSTDIR\uninstaller.exe


; レジストリに追加して「プログラムと機能」or「プログラム」に登録する
WriteRegStr HKLM ${RegistryKey} "DisplayName" "TSP:Travelling Salesman Problem"
WriteRegStr HKLM ${RegistryKey} "UninstallString" '"$INSTDIR\uninstaller.exe"'
WriteRegStr HKLM ${RegistryKey} "Publisher" 'uncorrelated@yahoo.co.jp'
WriteRegStr HKLM ${RegistryKey} "DisplayVersion" '1.0'


SectionEnd ; end the section


; アンインストール時の挙動
Section "Uninstall"


; ファイルを消す
Delete $INSTDIR\TSP.exe
Delete $INSTDIR\readme.txt
Delete $INSTDIR\TSP_ja_JP.qm


; システム・ディレクトリからDLLを消す
!insertmacro UnInstallLib DLL SHARED REBOOT_NOTPROTECTED $SYSDIR\QtCore4.dll
!insertmacro UnInstallLib DLL SHARED REBOOT_NOTPROTECTED $SYSDIR\QtGui4.dll
!insertmacro UnInstallLib DLL SHARED REBOOT_NOTPROTECTED $SYSDIR\libgcc_s_dw2-1.dll
!insertmacro UnInstallLib DLL SHARED REBOOT_NOTPROTECTED $SYSDIR\mingwm10.dll


; アンインストーラーも消去
Delete $INSTDIR\uninstaller.exe


; ディレクトリ消去。なお/rをつけると再帰的に、/REBOOTOKをつけると再起動時に消す。
RMDir $INSTDIR


; スタートメニューのショートカットを消す
Delete "$SMPROGRAMS\$(ShortcutDirectory)\TSP.lnk"
Delete "$SMPROGRAMS\$(ShortcutDirectory)\uninstaller.lnk"
RMDir "$SMPROGRAMS\$(ShortcutDirectory)"


; レジストリを消しておく
DeleteRegKey HKLM "Software\Microsoft\Windows\CurrentVersion\Uninstall\TSP"


SectionEnd

TSPInstaller.nsiと言うファイル名で保存しました。

4. 日英のライセンス・ファイルを記述する

国際化しているので、license-english.txtとlicense-japanese.txtを用意します。動かすだけなら、空ファイルでも構いません。

5. コンパイルする

以下のようにコンパイルします。

makensis TSPInstaller.nsi

これでTSPInst.exeが生成されます。

6. TSPInst.exeを動かす

動かすと以下のような今風ではない殺風景なインストーラーが起動します。

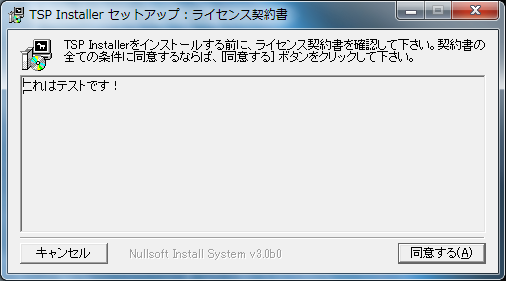
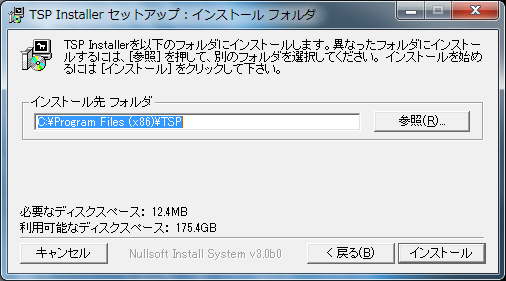
7. インストール状態を確認する

%PROGRAMFILES%\TSP以下にファイルがちゃんと展開されています。

DLLはC:\Windows\SysWOW64以下に配置されました。

これでスタート・メニューから起動とアンインストールができます。

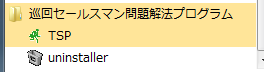
また、「プログラムと機能」からアンインストールが可能になって、Windowsアプリケーションらしく見えます。

8. まとめ

小さなアプリケーションだと、いちいちインストールするよりもZIPファイルを展開したら使えるようにして欲しいと言われることもあるのでインストーラーを用意する必要性は無い事も多いのですが、たまにインストーラーを要望される事もあります。Windows環境でのNSISはWinampの他、OpenOfficeなどでも実績があり、国際化に対応していたり、外部実行ファイルを呼び出せたりと何かと高機能なので、そういう時は有力な選択肢の一つになると思います。
付属ドキュメントが英語で、ドキュメント中の例が部分的なところが扱いづらいと感じるかも知れませんが、付属のサンプル・ソースコードやオンライン・ドキュメントを検索して完全版のソースコードを見ていると分かることも多いので、オープンソースのツール等でWindowsアプリケーションを作っていてインストーラーを書く必要に迫られている人は、ぜひトライしてみてください。

*1:オープンソース／フリーソフトのWiXを使う選択肢もありますが、宗教的理由などで.NETを使いたくない時もあります。

ポアソン回帰で推定しているモノはλの式

R言語

某所の(1)ポアソン回帰モデルの説明が、(2)対数変換OLSと同じになっている気がします。違うものだと思うのですが、シミュレーションをして(1)と(2)の推定をして確認してみました。

1. モデル

ポアソン分布はパラメーター\lambdaで決定されるわけですが、\lambdaを説明変数で説明するモデルになります。n個のパラメータがあり、xを説明変数、\betaを係数として、以下のような式ですね。
\lambda = e^{\beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_n x_n}
P(y=k) = \frac{\lambda^k e^{-\lambda}}{k!}
被説明変数yの値が0以上の整数kのときの確率を、xは間接的に決定するわけですね。教科書的には最尤法を用いて求めることになるみたいですが、実用的にはリンク関数を用いて一般化線形回帰モデルで推定できるようです。

2. データ作成

まずはポアソン回帰モデル用のデータxとyを作成します。

set.seed(20130919)
x <- round(runif(100, max=3))
lambda <- exp(1.1 + 1*x)
y <- numeric(length(x))
for(i in 1:length(x)){
  y[i] <- rpois(1, lambda[i])
}

3. Rで推定してみる

glm関数を使うだけですけど、推定できます。

r_pois <- glm(y ~ x, family=poisson)
summary(r_pois)

4. 対数変換OLSと比較してみる

比較のために、対数変換OLSをかけてみましょう*1。

r_ols <- lm(log(y) ~ x)
summary(r_ols)

当たり前ですが、残差平方和も異なります。

sum((y - fitted.values(r_pois))^2)
sum((y - exp(fitted.values(r_ols)))^2)

5. over-dispersionのテスト

tの切片項が0を棄却されたら、つまり有意に0以外ならばover-dispersionでポアソン分布でないことになります。

t <- fitted.values(r_pois)
z <- ((y - t)^2 - y)/(t*sqrt(2))
summary(lm(z ~ 0 + t))

人工的なデータなのですが、P値が0.323でした。

*1:実は対数化できるようにyはゼロ以上の数字になっています。

Rのグラフに回帰分析の結果である数式を書き込む

R言語

データをプロットしたグラフに、推定された予測値や、推定されたパラメーターを数式ごと書き込みたいときはありませんか？
そう難しい話では無いのですが、幾つかコツがあるので例を作ってみました。

1. データセット

グラフを描くにはデータセットが要るので、今回は以下の数字を

# 奈良女子大学のページにあった実験観測データを拝借
t <- c(0,5,10,15,20,25,30) # 時間
Ts <- c(56.5, 32.1, 21.9, 17.0, 14.6, 11.9, 10.9) # 物体の温度
Tm <- 0 # 外気温（冷却材は氷でゼロ度だが、室温はもっと高い模様。なお、9.660583度を仮定すると、もっとも当てはまりが良い）

2. 推定を行う

推定を行い、予測値を計算してみましょう。モデルの制約によりpredict関数は使えません。

# ニュートンの冷却の法則を想定し、定数を推定する
dT <- (Ts - Tm)/(Ts[1]- Tm)
# OLSで推定。
r <- lm(log(dT) ~ t + 0)
# 予測値を計算
prdct <- Tm + (Ts[1] - Tm)*exp(coef(r)[1]*t)

3. プロットする座標の範囲を決める

グラフを重ねる前に縦横の座標の範囲を決めておかないと、ズレます*1。

xlim <- c(0, max(t))
ylim <- c(0, 100)

4. データをプロットする

まずは観測値をプロットしてみます。

par(mar=c(5, 3.5, 1, 1), mgp=c(2, 1, 0))
plot(Ts ~ t, xlab="経過時間", ylab="", axes=FALSE, xlim=xlim, ylim=ylim)
x_at <- seq(xlim[1], xlim[2], 10)
y_at <- seq(ylim[1], ylim[2], 25)
x_labels <- sprintf("%d分", x_at)
y_labels <- sprintf("%d℃", y_at)
axis(1, at=x_at, labels=x_labels, pos=ylim[1])
axis(2, at=y_at, labels=y_labels, pos=xlim[1], las=2)

5. 推定値を重ね書きする

推定値をグラフに書き込みます。ここはRの紹介で良く触れられますね。

par(new=T)
plot(prdct ~ t, type="l", xlab="", ylab="", axes=FALSE, xlim=xlim, ylim=ylim, lty=2)

なお、こんな手間隙かけずにlines(t, prdct, lty=2)するべきだろと突っ込まれました。おっしゃる通り。
直線なのが気に入らない人は、plotの代わりに以下のようにcurveを使ってください。

par(new=T)
curve(Tm + (Ts[1] - Tm)*exp(coef(r)[1]*t), xname="t", xlab="", ylab="", axes=FALSE, xlim=xlim, ylim=ylim, lty=2)

6. 推定された式を凡例として表示する

まず、数式をsprintf関数で作って、parse関数で表現式に変えます。expression関数は、代入が手間なので使いません。使える数式の記号はhelp plotmathをすると一覧が見られます。

expr <- parse(text = sprintf("%.3f + (%.3f-%.3f)*e^{%1.3f*t}", Tm, Ts[1], Tm, coef(r)[1]))

次に、legend関数で凡例を表示します。推定値はlty、観測値はpchになりますが、使わない方には-1を入れていることに注意してください。

legend("topright", lty=c(2, -1), pch=c(-1, 1), legend=c(expr, "観測値"), bty="n")

7. データの出所を明記する

データを拝借しているので、出所を明記しておきましょう。

mtext("出所) 奈良女子大 - 「第11回の授業　(07/07/09)」の実験データから編集" , side=1, line=3.5, adj=0)

8. 完成図

相関係数などを書いても良かったかも知れません。

9. 補足

文字が化ける場合は、以下のようにpar()関数で指定するグラフィックス・パラメーターでフォントを指定してください。フォントはMeiryoを指定していますが、お使いのOSにあわせましょう。

windowsFonts(GraphFont = windowsFont("Meiryo"))
par(mar=c(5, 3.5, 1, 1), mgp=c(2, 1, 0), family="GraphFont")

画面のグラフを保存したい場合は、以下のような感じで。

dev.copy(png, "ニュートンの冷却の法則の実験結果.png", width=640, height=480, bg="white")
dev.off() # 画面のグラフを消す
dev.off() # PNGファイルを閉じる

*1:推定値のプロットにpar(new=T)とplot()を使うからズレるのであって、低水準関数のlines()を使えば座標の範囲を決めなくてもいいと言うツッコミがありましたが、ここを決めておかないと軸目盛などの位置もズレると言うか、あわせるのが困難になるので、やはり決めておいた方がいいです。

Rのグラフ中文字列の上下左右の寄せ

R言語

text関数でプロット領域に文字を書き込むことができるわけですが、指定座標と文字位置の関係を示すadjパラメーターの意味を整理してみます。
グラフの中心に表示座標をとり、adjだけ色々と変えてみたグラフが以下です。

  • c(1, 0)だと、文字列の右下に表示座標が来ます。
  • c(0, 0)だと、文字列の左下に表示座標が来ます。
  • c(0, 1)だと、文字列の左上に表示座標が来ます。
  • c(1, 1)だと、文字列の右上に表示座標が来ます。

0.5を入れておくと中央になるわけですね。1を超えた値や、マイナスの値も有効です。
mtext関数のadjはベクトルではなく、値一つのスカラー値になるので注意してください。上下寄せを指定できません。

Rのグラフで余白の調整

R言語

Rのプロットはデフォルトでは余白が多いです。しかし、TeXの方でタイトルや注釈を入れる場合は、プロット領域を大きく取りたくなるので、この余白を削りたくなります。par関数のmar、mgpオプションで余白を調整できるので覚えておきましょう。

1. marオプション

marオプションは、下・左・上・右の余白を指定します。

デフォルトでは以下のようになっていますが、タイトルや注釈・出所の有無で調整した方が良いでしょう。

par(mar=c(5, 4, 4, 2) + 0.1)

単位はmexで行の高さです。

2. mgpオプション

mgpオプションは軸ラベル・軸メモリ・軸線の位置を指定します。

デフォルトでは以下のようになっていますが、軸ラベルの位置がプロット領域から遠すぎるので、c(2.5, 1, 0)ぐらいを指定した方が幸せになれると思います。

par(mgp=c(3, 1, 0))

単位はmexで行の高さです。

3. タイトル

plot関数でmainオプションを指定しないで、plot後にtitle関数でlineオプションをつけるのが良いようです。

title(main="グラフの表題", line=1)

Rで多体問題を数値解析

R言語

古典物理学と言えばニュートンの運動方程式で、何かの軌道をプロットするのが定番です。三体以上の問題は特殊なケースしか閉じた解が出てこないので、数値解析が行われています。銀河にある星の数をシミュレーションすると、スーパーコンピューターな数値演算能力が必要な世界になるわけですが、二個や三個であればPC上のRで計算できるので、試しにやってみましょう。

1. 計算する式

まずは物理の教科書に書いてありそうなニュートンの運動方程式の確認から*1。

m_i \frac{d^2r_i}{dt^2}=-\sum^n_{j=1,j \neq i}G\frac{m_i m_j}{r^2_{ij}}

Gが万有引力定数、mが質量、rが距離、nは質点の数、iは質点、tが時点を表します。
力の成分をxとyに分解します。z成分は省略。

m_i \frac{d^2x_i}{dt^2}=-\sum^n_{j=1,j \neq i}G\frac{m_i m_j}{r^2_{ij}} \cdot \frac{x_j-x_i}{r_{ij}}

m_i \frac{d^2y_i}{dt^2}=-\sum^n_{j=1,j \neq i}G\frac{m_i m_j}{r^2_{ij}} \cdot \frac{y_j-y_i}{r_{ij}}

r_{ij} = \sqrt{(x_j-x_i)^2 + (y_j-y_i)^2}

両辺をm_iで割って、x2=\frac{d^2x_i}{dt^2}、y2=\frac{d^2y_i}{dt^2}と置いて、常微分方程式に変形しましょう。

x_1=\frac{dx_i}{dt}
y_1=\frac{dy_i}{dt}
x_2=-\sum^n_{j=1,j \neq i}G\frac{m_j}{r^2_{ij}} \cdot \frac{x_j-x_i}{r_{ij}}
y_2=-\sum^n_{j=1,j \neq i}G\frac{m_i m_j}{r^2_{ij}} \cdot \frac{y_j-y_i}{r_{ij}}

これをルンゲ＝クッタ法などで計算します。二体問題でも解析解を出すのには色々と苦労するので、手抜きな感じがたまりません。

2. ソースコード

N=3でも4でもいいのですが、N=2のソースコードを提示します。まずは演算部分。

# deSolveパッケージを使います
library("deSolve")


# 常微分方程式化したモデル
model <- function(t, X, params){
  with(as.list(params),{
    # 引数を分解
    x <- X[1:n]
    y <- X[(n+1):(2*n)]
    dx1 <- X[(2*n+1):(3*n)]
    dy1 <- X[(3*n+1):(4*n)]
    # 戻り値の領域を確保
    dx2 <- numeric(n)
    dy2 <- numeric(n)
    for(i in 1:n){
      r3 <- sqrt((x[-i]-x[i])^2+(y[-i]-y[i])^2)^3
      dx2[i] <- sum(-G*m[-i]*(x[-i]-x[i])/r3)
      dy2[i] <- sum(-G*m[-i]*(y[-i]-y[i])/r3)
    }
    list(c(dx1, dy1, dx2, dy2))
  })
}


# 計算のループ条件。0.1刻みで250まで。
times <- seq(0, 250, 0.1)
# 質点の数
n <- 2
# 質点の重さ
m <- c(500, 1)
# 初期座標と初期速度を以下の並び順で指定
# x[1], x[2], y[1], y[2], dx[1], dx[2], dy[1], dy[2]
X <- c(100, 400, 100, 400, 1, -1, 1, 0)
# 常微分方程式として計算する
out1 <- ode(X, times, model, parms = list(n=n, G=-9.80665, m=m), method="rk4")

演算結果は数値の羅列で分かりづらいので、グラフにしましょう。

# プロット範囲を指定
xlim <- c(0, 800)
ylim <- c(0, 800)


# N時点までのプロット
plot_as_of_N <- function(N){
  plot(out1[,2][1:N], out1[,2+n][1:N], xlim=xlim, ylim=ylim, type="l", xlab="x", ylab="y", lty=2)
  for(i in 2:n){
    par(new=T)
    plot(out1[,i+1][1:N], out1[,i+1+n][1:N], xlim=xlim, ylim=ylim, type="l", lty=i+1, xlab="", ylab="", main=paste("t=", round(N)))
  }
  for(i in 1:n){
    points(out1[N,i+1], out1[N,i+1+n], pch=i, cex=2)
  }
  legend("topleft", lty=seq(2, length(m)+1), legend=sprintf("m=%d", m), bty="n")
}


# 同時に2×2個をプロット
par(mfrow = c(2,2), oma = c(0, 0, 0, 0))
for(i in seq(1, length(out1[,1]), (length(out1[,1])-1)/3)){
  plot_as_of_N(i)
}

z軸を加えたり、質点の数を増やすのは難しく無いと思います。例えば以下のように三つのパラメーターをいじれば、三体問題化できます。

n <- 3
m <- c(500, 2, 1)
X <- c(100, 400, 800, 100, 400, 0, 1, -1, 0, 1, 1, 0)

衝突処理が無いので質点が近づきすぎると、どこかに飛んで行くのでパラメーターの設定には注意してください。

3. 計算結果

パラメーターに大きく依存するわけですが、上のコードだと下のようなグラフが描けます。最近は波ばかりプロットしていたので、グルグルしていて爽快ですね。

なおオイラー法などで計算すると、誤差が大きくなって全く違う図になります。

*1:詳しい説明は富久(2010)の第5章を参照

RでKdV方程式を数値解析でプロットしてみる

R言語

浅水波を表すKdV方程式は、今では可積分系として閉じた解が知られている非線形偏微分方程式ですが、これは意外に最近知られるようになった事で、二十世紀の中ごろにザブスキーとクルスカルと言う物理学者がシミュレーションをしてソリトンと言う孤立波を見つけ、そこから解析が大きく進むようになったそうです（武部(2008)）。当時を偲んでRで数値計算してみましょう。

1. KdV方程式の形状

まずは式の確認です。

\frac{\partial}{\partial t} u(t,x) + 6u(t,x)\frac{\partial}{\partial x}u(t,x) + \frac{\partial^3}{\partial x^3} u(t,x) =0

tが時間、xが位置、u(t,x)が波の高さになります。
このKdV方程式は、例えば波動方程式と比べると厄介な形状をしています。三階微分が中にあり、数値演算のお決まりのパターンである常微分方程式にならないのです。

2. 数値演算が出来る形に変形する

どうしたら良いのかな・・・と思っていたら、Numerical Solution of the KdVと言うページに全てのノウハウが書いてありました。
まずは第二項を整理します。合成関数の微分を思い出すと何をしているのか分かります。

\frac{\partial}{\partial t} u(t,x) + 3\frac{\partial}{\partial x} u(t,x)^2 + \frac{\partial^3}{\partial x^3} u(t,x) = 0

ここでフーリエ変換を思い出します。Rやmatlabで使われる式とは周期と積分範囲が異なるので注意してください。

F\bigg(u(k) \bigg ) = \hat{u(k)} = \int^{\infty}_{-\infty} u(x) e^{-ikx} dx

フーリエ変換をかけます。公式により虚数iとkでxの偏微分を無くす事ができます。

\frac{\partial}{\partial t} \hat{ u(k) } + 3ik \hat{ u(k)^2 } - ik^3 \hat{ u(k) } = 0

この式はスプリット・ステップ法（the split step method）で計算する事ができます。

\frac{\partial}{\partial t} \hat{ u(k) } = - 3ik \hat{ u(k)^2 } + ik^3 \hat{ u(k) }

オイラー法で \Delta tを用いて書くと以下のようになります。

\hat{ u_1(k, t + \Delta t) } = \hat{ u(k, t) } e^{ik^3 \Delta t}

\partial \hat{u}/\partial t \cdot 1/\hat{u}=ik^3の形にして、両辺をtで積分し、対数を消してu(k, t)=C e^{ik^3 t}の形に整理してから、u(k, t + \delta t)を計算していますね。

\hat{ u(k, t + \Delta t) } = \hat{ u_1(k, t + \Delta t) } - 3ik \Delta t \hat{ u_1(k, t + \Delta t)^2 }

上式の右辺第二項のフーリエ変換周りは注意してください。

\hat{ u(k, t + \Delta t) } = \hat{ u_1(k, t + \Delta t) } - 3ik \Delta t F [ F^{-1} [ \hat{ u_1(k, t + \Delta t)^2 } ] ]

フーリエ変換、逆フーリエ変換、フーリエ変換の三段構えです。

3. ソースコード

matlabのコードをRに翻訳した感じですが、意外に短いコードで計算する事ができます。計算速度は・・・遅いですね。なお精度はイマイチなので、ルンゲ＝クッタ法などに書き直した方が良いかも知れません。

# 補助的に使う関数
cosh <- function(x){ (exp(x)+exp(-x))/2 }
sech <- function(x){ 1/cosh(x) }
phi <- function(x, t, k=1){
  2*k^2*sech(k*(x-4*k^2*t))^2
}
ifft <- function(x){ fft(x, inverse=TRUE)/length(x) }


# 初期値
N <- 256
x <- seq(-10, 10, length.out=N)


# 波の初期値
# ソリトン波を指定しているが、他のモノでも良い
u1 <- phi(x, -1)


# 変化幅
delta_x <- x[2] - x[1]
delta_t <- 10/N^2 # エラーが出る場合は0.4/N^2で
# フーリエ変換の定義による周期の違いを2*piで調整
delta_k <- 2*pi/(N*delta_x)


# 離散フーリエ変換ではkの値が不連続になるので注意
# 参考: http://www.made.gifu-u.ac.jp/~tanaka/LectureNote/numerical_analysis.pdf P.109
k <- c(seq(0, N/2*delta_k, delta_k), seq(-(N/2-1)*delta_k, -delta_k, delta_k))


# t=1までnmax回波を動かす
tmax <- 1
nmax <- round(tmax/delta_t)
U = fft(u1)
for(n in 1:nmax){
  # first we solve the linear part
  U = U*exp(1i*k^3*delta_t)
  # then we solve the non linear part
  U = U - 3i*k*delta_t*(fft(Re(ifft(U))^2))
}
# 変化後の波を得る
u2 <- Re(ifft(U))


# 元と変化後の波を描画する
xlim = c(0, N)
ylim = c(0, max(u1, u2))
plot(u1, xlim=xlim, ylim=ylim, type="l", lty="dotted", xlab="x", ylab="u(t, x)", main="KdV方程式のプロット")
par(new=T)
plot(u2, xlim=xlim, ylim=ylim, type="l", xlab="", ylab="")
legend("topleft", lty=c(3, 1), col=c("black", "black"), legend=c("t=0", "t=1"))

4. 計算結果

アニメーションさせる気がしないぐらい時間がかかるので、2時点だけで。