ノイズが多い時系列データに対しては、観測値から観測誤差を取り除いて、分析者の興味関心である観察不能な状態を取り出すカルマンフィルターがよく使われています。しかし、カルマンフィルタは線形近似になるため、より一般的に用いることができるアルゴリズムとして粒子フィルタが開発されていて、カルマンフィルタほどではないですが様々な分野で利用されています。
矢野 (2014)「粒子フィルタの基礎と応用:フィルタ・平滑化・パラメータ推定」によると、粒子フィルタは1980年代に原案があり、1990年代に提案された相対的に新しい手法です。検索をすると、ここ5年間でも手法の改善を提案する論文があります。一方で、計算手順は簡素で実装しやすいものです。計算時間や記憶装置がカルマンフィルタよりも多く必要になりますが、イマドキの計算機にとっては誤差みたいなもんになっています*1。
さて、プログラマ的にはコードを走らせて感覚を掴みたいわけですが、目についた例は簡素すぎました。粒子フィルタはシステム誤差を乱数で生成し、観測誤差を尤度関数で測って推定を行なうのですが、例ではこの2種類の乱数の確率密度関数のパラメーターが定数で与えられています。しかし、事前にシステム誤差と観測誤差のパラメーターを知ることはできないので、応用によっては実用的に思えないものになっています。
粒子フィルタではパラメーターの状態を考える事により、パラメーターの推定も同時に行なう事ができます。実用ではパッケージを使う方がよいですが、何をやっているか把握してみましょう。状態変数はコーシー分布か一様分布に従うシステムノイズによって変化し、観測値には正規分布に従う誤差が入る、状態変数がの3つ、観測値が
の1つの推定モデルを考えて推定します。
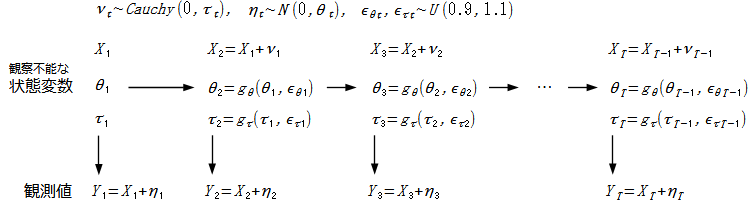
1. データセット
Kitagawa (1998)の最初の例なのですが、不連続な状態遷移と正規分布する観測誤差を仮定してデータを生成します。なお、推定モデルのシステムノイズの仮定には沿っていません。
set.seed(406149) # t: 観察不能な状態 # T: 分析期間の長さ # y: 観測値 t <- rep(c(0, 1.5, -1, 0), each = 100) T <- length(t) y <- rnorm(T, mean = t, sd = 1)
2. 粒子フィルタで推定
計算自体は50行かからないぐらいで終わります。パッケージで実装されているものは、もっと複雑なことをしていると思いますが。なお、パラメーターの状態変数のシステムノイズが変則的に入れてありますが、パラメーターが0以下にならないようにです。
# 仮定するsystem noiseのνはコーシー分布 nu <- function(location, log_tau2) rcauchy(length(log_tau2), location = location, scale = sqrt(10^log_tau2)) # 観測誤差は正規分布 calcWeights <- function(y, x, sd){ p <- dnorm(y, mean = x, sd = sd) p / sum(p) } # M: 各期でサンプリングする数 # x: 各期でサンプリングした値 # log_tau2: 各期でサンプリングに使う分布のパラメーター/x[i,j]ごとにある/log(tau^2, 10) # w: 各期でリサンプリングに使うウェイト/尤度 # sd: 観測誤差の標準偏差 M <- 201 # 初期値を設定 w <- theta <- log_tau2 <- x <- matrix(NA, M, T) log_tau2[, 1] <- runif(M, min = -8, max = -2) theta[, 1] <- runif(M, min = 1e-6, max = 2) x[, 1] <- rnorm(M, sd = 4) # 始点のウェイトは雑につくる w[, 1] <- calcWeights(y[1], x[, 1], sd = theta[, 1]) # パラメーターの誤差を大きくして、縮退しないようにする関数 g <- function(x) x*runif(M, min = 0.9, max = 1.1) # フィルタリング分布を計算 for(j in seq(2, T)){ # 予測分布をつくる x[, j] <- nu(x[, j - 1], log_tau2[, j - 1]) # リサンプリング用のウェイトをつくる w[, j] <- calcWeights(y[j], x[, j], sd = theta[, j - 1]) # リサンプリング i <- sample.int(M, replace = TRUE, prob = w[, j]) x[, j] <- x[i, j] # パラメーターは縮退防止で粒子のばらつきを増している log_tau2[, j] <- g(log_tau2[i, j - 1]) theta[, j] <- g(theta[i, j - 1]) }
3. プロット
推定結果を図示してみましょう。
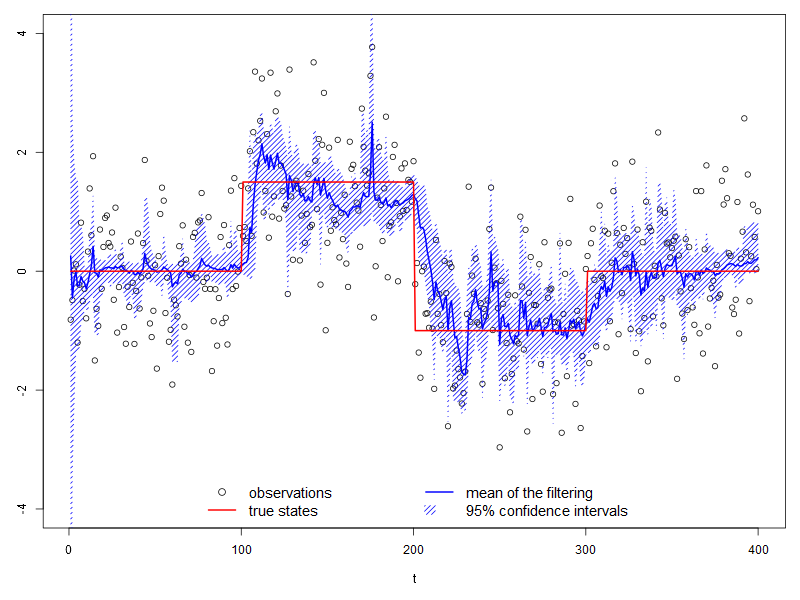
3.1. フィルタリング分布
完璧とは言えませんが、観測誤差がだいぶ取れているのが分かります。
x_mean <- apply(x, 2, mean) x_quantiles <- apply(x, 2, function(x) quantile(x, probs = c(0.025, 0.975))) par(cex = 1, cex.lab = 1, cex.axis = 1, cex.main = 1, mar = c(5, 3, 1, 1)) plot(y, xlab = "t", ylab = "", ylim = c(-4, 4)) lines(x_mean, col = "blue", lwd = 2) polygon(c(1:T, T:1), c(x_quantiles[1, ], rev(x_quantiles[2, ])), density=20, col="blue", border=NA) lines(t, col = "red", lwd = 2) legend("bottom", c("observations", "true states", "mean of the filtering", "95% confidence intervals"), ncol = 2, bty = "n", inset = 0.00, cex = 1.25, lty = c(NA, 1, 1, NA), lwd = c(1, 2, 2, NA), pch = c(21, NA, NA, NA), fill = c(NA, NA, NA, "blue"), density = c(0, 0, 0, 20), border = NA, col = c("black", "red", "blue", "blue"))
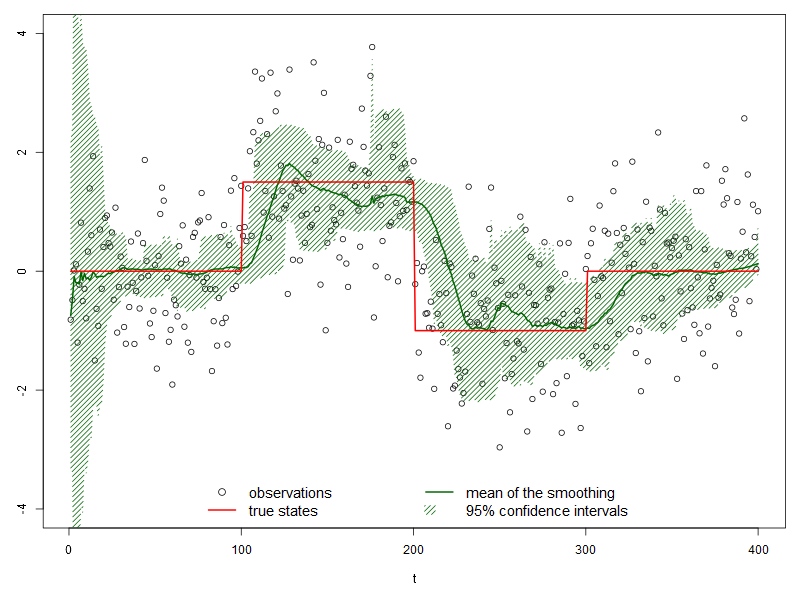
3.2. 平滑化分布
構造的にはフィルタリング分布と同じなのですが、過去の粒子も推定に用いることで滑らかにします。
# 平滑化分布を計算 L <- 20 s <- matrix(NA, M*L, T) for(j in 1:T){ columns <- max(1, j - L + 1):j i <- sample.int(M, replace = TRUE, prob = w[, j]) tmp <- sapply(columns, function(k){ x[i, k] }) s[1:length(tmp), j] <- tmp } s_mean <- apply(s, 2, mean, na.rm = TRUE) s_quantiles <- apply(s, 2, function(x) quantile(x, probs = c(0.025, 0.975), na.rm = TRUE)) par(cex = 1, cex.lab = 1, cex.axis = 1, cex.main = 1, mar = c(5, 3, 1, 1)) plot(y, xlab = "t", ylab = "", ylim = c(-4, 4)) lines(s_mean, col = "darkgreen", lwd = 2) polygon(c(1:T, T:1), c(s_quantiles[1, ], rev(s_quantiles[2, ])), density=20, col="darkgreen", border=NA) lines(t, col = "red", lwd = 2) legend("bottom", c("observations", "true states", "mean of the smoothing", "95% confidence intervals"), ncol = 2, bty = "n", inset = 0.00, cex = 1.25, lty = c(NA, 1, 1, NA), lwd = c(1, 2, 2, NA), pch = c(21, NA, NA, NA), fill = c(NA, NA, NA, "darkgreen"), density = c(0, 0, 0, 20), border = NA, col = c("black", "red", "darkgreen", "darkgreen"))
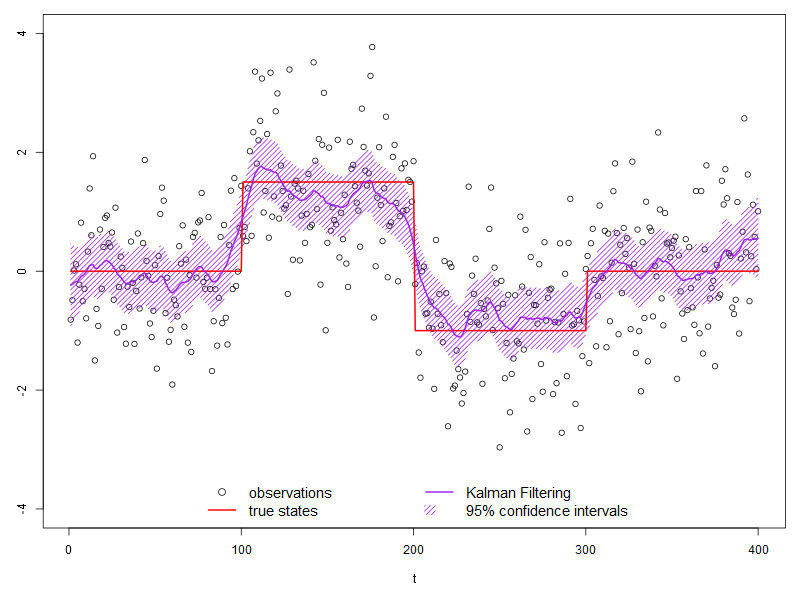
4. カルマンフィルターとの比較
以下はKFASパッケージで計算したものですが、上で雑に計算した粒子フィルタの方が予測誤差は大きく、偏りが少なくなっています。この例だとカルマンフィルターに対する優位性は恐らくないです。
*1:組み込み用途ではつらいかも知れません。