特定月の分散が大きいときの大数の法則

別のブログで使った大数の法則を示すシミュレーションのソースコードです。

# 乱数から分析データを作る
set.seed(20150209)
x.sd <- 16.96534 # 想定標準偏差
n <- 24 # 分析年数
x <- as.numeric(n*12) # 分析データ
for(i in seq(1, (n-1)*12, 12)){
  x[i:(i+11)] <- c(rnorm(3, sd=x.sd), rnorm(1, sd=x.sd*2), rnorm(8, sd=x.sd))
}

# 分析データの状態を確認
plot(x, type="l", main="集計前データ", xlab="", ylab="")

# n年分を合計してプロットする
x.sum <- numeric(12)
for(i in 1:(n-1)){
x.sum <- x.sum + abs(x[(i*12-11):(i*12)])
}
max <- (as.integer(max(x.sum)/n/5)+1)*5
B <- barplot(x.sum/n, names.arg=sprintf("%d月", 1:12), ylim = c(0, max), main=sprintf("シミュレーション（%d年分）", n))

# 偏差値を計算してみる
y.mean <- mean(x.sum/n)
y.sd <- sd(x.sum/n)
sprintf("4月の偏差値: %.2f", ((x.sum/n)[4]-y.mean)/y.sd*10+50)

Rで各集団における大きい方から2番目の値を調べる

ツイッターで見かけた御題なのですが、（学校の課題などで）ありそうなので、置いておきます。

# お試しデータを作る
set.seed(20150208)
n <- 30
df <- data.frame(type=c("A", "B", "C")[round(runif(n, min=0.5, max=3.5))], value=60 - ((1:n)-10)^2)

# タイプごとに最大値を求める
tapply(df$value, df$type, max)

# 2番目の値を求める
tapply(df$value, df$type, function(x){
  # 降順ソートをして2番目を返す
  # 最大値が複数ありえる場合は、後述の「最大値を除外する: O(n)が2回」のコードか、追記したコードを使ってください
  sort(x, decreasing=TRUE)[2]
})

奥村晴彦氏から計算量がO(n log n)でオセーヨってツッコミが来たので、O(n)になるように改良してみましたが、300万件でもuserで2割ぐらいしか時間を削れませんでした*1。小選挙区の数は300しかないので（謎）、遅いコードで許してください。
以下は時間計測に使ったコードです。

set.seed(20150208)

# 300万件でテスト
n <- 3000000

# データは散らばるようにしておく
df <- data.frame(type=c("A", "B", "C")[round(runif(n, min=0.5, max=3.5))], value=runif(n, min=0, max=n))

# ソートする遅い版: O(n log n)
gc();gc();system.time({
  tapply(df$value, df$type, function(x){
   sort(x, decreasing=TRUE)[2]
  })
})

# 最大値を除外する: O(n)が2回
gc();gc();system.time({
  tapply(df$value, df$type, function(x){
    max( x[x!=max(x)] )
  })
})

# コメントで示唆されたもの: O(n)が2回
gc();gc();system.time({
  tapply(df$value, df$type, function(x){
    x[which(x==max(x))] <- NA;
    max(x, na.rm=TRUE)
  })
})

追記(2018年5月19日)

これでは同値で1位があったときに2番目に大きい数字が取れないと言う指摘があったので、（上述の最大値を除外する: O(n)が2回のコードでも良いのですが）max2関数を定義して正しく処理できるようにします。

# データセットを作る
set.seed(20180519)
df2 <- data.frame(type=c("A", "B", "C")[round(runif(n, min=0.5, max=3.5))], value=round(runif(n)*10))

# データセットのタイプ別の値をソートして並べ替える
tapply(df2$value, df2$type, sort)

#
# 2番目もしくはranking番目に大きい数字を戻す関数
# 該当がなければNA
#
max2 <- function(x, ranking=2){
  y <- sort(x, decreasing=TRUE)
  m <- ranking
  p <- 1
  while(1<m && p<length(y)){
    if(y[p]>y[p+1]){
      m <- m - 1
    }
    p <- p + 1
  }
  if(1<m){
    return(NA)
  }
  y[p]
}

# 2番目を求める
tapply(df2$value, df2$type, max2)

# 3番目を求める
tapply(df2$value, df2$type, function(x){
  max2(x, ranking=3)
})

*1:3000万件でも3割ぐらいしか削れないので、Rのsort関数が速く、max関数が遅いんじゃないかと言う疑惑が・・・

時系列データの季節調整をしてみよう

時系列データには、季節バイアスが入りがちです。年中行事はもちろんのこと、天候の変化も周期的に発生します。ゴールデンウィークのある5月よりも6月の方が行楽客が少ないとしても、行楽客が減少し出したとは言えないでしょう。そもそも月ごとに日数も異なりますし。月次データを見るときは、季節バイアスの影響を考慮する必要があります。これを数字の処理で行なうのが、季節調整です。実際にRで試してみて、どのぐらい調整できるか見てみましょう。単純移動平均とloessアルゴリズムを用います。

1. 精度を確認する手順

実データでは季節バイアスがどれぐらい入っているのか真実は誰も知らないので、季節バイアスが入った擬似データを作成します。二次方程式から作った非季節変動値に、乱数から作った真の季節バイアスを加えて、観測データを作ります。この観測データを処理して計算された季節バイアスを取り出し、真の季節バイアスと就き合わせてみましょう。

2. 擬似データを作成する

1996年1月から60ヶ月の月次データとして、12ヶ月周期の擬似データを作成します。

# 結果が同じになるように乱数シードを固定
set.seed(20150119)

# 12ヶ月5年分で観測数60
n <- 12*5

# 季節バイアスを乱数から生成
s_bias <- runif(12, min=0, max=4)
# 平均0に正規化しておく
s_bias <- s_bias - mean(s_bias)

# 季節バイアスを連結して、5年分の季節変化をつくる
# tsで時系列データ型にしておく
s_chg <- ts(rep(s_bias, 5), start=c(1996, 1), frequency=12)

# 二次方程式から非季節変動値を作る
x <- 1:n
e <- 0 # 誤差はゼロとしておく。入れるときは rnorm(n) などn個のベクトルを指定。
nsv <- ts(0.9 + 0.003*(x-2*n/3)^2 + 0.1*x, start=c(1996, 1), frequency=12)

# 非季節変動値と季節バイアスを足して、原数値を作成する
y <- ts(nsv + s_chg + e, start=c(1996, 1), frequency=12)

3. 単純移動平均

12ヶ月の算術平均をとる単純移動平均は、単純な計算の割りには効果的に季節バイアスを除去します。最初の11ヶ月はデータが無い欠損値になること、非季節変動値に変化があってから効果が見えるのが遅れことが欠点になりますが、目視するには悪く無いです。

# 移動平均
# 最初11ヶ月分の値はでない。
ma <- ts(numeric(n-11), start=c(1996, 12), frequency=12) # グラフを描くために、時系列データ型にしておく
for(i in 12:n){
  ma[i-11] <- mean(y[(i-11):i])
}

4. loessアルゴリズム

Rの組み込み関数stl()で使えるloessアルゴリズムは、局所重み付け回帰関数を用いた高機能な季節調整方法です。ここでは詳しい手順は考えずに、Rに計算させましょう。なお、引数で与える変数が時系列データ型でないと動いてくれないので、注意してください。

stl.y <- stl(y, s.window="periodic")

5. グラフを描いて比較してみる

どれぐらいの精度で季節変動を補正できるのか、グラフを描いて比較してみましょう。この例では、かなりの精度で一致します。移動平均も遅れて動くわけですが、十分機能することが分かります。

plot(nsv + e, ylim=c(0, 10), main="季節調整方法の精度", lwd=2, xlab="", ylab="")
lines(y, lty=2, lwd=1)
lines(y - stl.y$time.series[,1], lty=3, col="red", lwd=2)
lines(ma, lty=4, col="blue", lwd=2)

legend("topleft", c("真の非季節変動値", "原数値", "loessアルゴリズム", "12ヶ月移動平均"), col=c("black", "black", "red", "blue"), lty=c(1, 2, 3, 4), lwd=c(2, 1, 2, 2), bg='white', box.col = 'black', bty="n")

ただし、これは非季節変動値が滑らかな二次関数だからで、ゼロにしている誤差が大きくなると当てはまりが悪くなります。季節変動の標準偏差と同じ大きさの標準偏差を持つ誤差項を入れると、トレンドの変化を掴むのに問題があるほどでは無い*1ですが、真の値と計算値の乖離は目で見て分かる程度になります。

6. X-12-ARIMA

最近はX-13-ARIMAが出てきたようですが、官公庁などでは米国商務省が開発した移動平均型季節調整法であるX-12-ARIMAを使っています。これはアプリケーションが配布されていて、Rからも扱うためのx12パッケージもあります。
Windows機の場合、C:/WinX12にX-12-ARIMAを置いたら、Rでx12パッケージをインストールしたあと、以下のように使います。

library("x12")
x12path("C:/WinX12/x12a/x12a.exe")
x12.y <- x12(y)
# 季節調整値を表示
slot(x12.y, "d11")

オプションや同時計算される系列が多いので扱いが難しいのですが、季節バイアスの変化にも対応できるし精度は高いです。何十年分の統計を抱えている官公庁以外、使い道が限られそうですが。

*1:実際、回帰分析を行なっても、真の値でy=0.003*x^2 - 0.14*x、loessアルゴリズムによる推定値でy=0.002998*x^2 - 0.1402*xとなり、ほとんど差が無い。

「年/月」の形式を月末日でDate型に変更

月次データで「年/月」と言う形式（e.g. 2013/11、2014/2）は良く見かけると思いますが、Rのread.table関数でデータフレームに読み込むと文字列型*1になってしまいます。日付型でないと、subset関数などで絞り込むときに不便ですね*2。しかし、as.Date関数はこの形式を日付型に変えてくれません。そこで、ちょっとした細工をしてみましょう。
日経平均.txtと言うファイルを読み込みます。

df1 <- read.table("日経平均.txt", header=TRUE, sep="\t")

中身は、こんな感じです。

年月	始値	高値	安値	終値
1994/01	17369.74	20229.12	17369.74	20229.12
1994/02	20416.34	20416.34	18931.39	19997.20
1994/03	20216.62	20677.77	19111.92	19111.92

as.Dateをすると、こんな悲劇に。日付がないのがいけない模様です。

as.Date(df1$年月,"%Y/%m")
[1] NA NA NA NA NA NA NA NA NA

gsubで置換して日付を足せば変換できます。

df1$年月日 <- as.Date(gsub("([0-9]+)/([0-9]+)", "\\1/\\2/1", df1$年月))

これをsubset(df1, 年月日>="2013-1-1" & 年月日<="2013-12-31")のように絞り込めます。

日付を月末にする

少し応用して、2013-12-31のように月末値を代入しましょう。月末日は毎月かわりますし、うるう年の処理もいることに注意してください。
まずは月始日*3で、Date型ではなく、POSIXlt型の変数を作ります。

tmpDate <- as.POSIXlt(gsub("([0-9]+)/([0-9]+)", "\\1/\\2/1", df1$年月))

tmpDate$yearで年から1900を引いたものが、tmpDate$monで月から1を引いたものが、tmpDate$mdayで日が取得できます。これから翌月の月始日の日付を作成します。12月の翌月は、年が一つ増えて、1月に戻ることに注意してください。

nextMonth <- ISOdate(tmpDate$year+1900+(tmpDate$mon+1==12)*1, ((tmpDate$mon+1) %% 12)+1, 1)

他の環境に習熟している人は、mktimeではなくISOdateかと思うかも知れません。
翌月の月始日の24時間前（=3600*24秒）が当月の月末です。

df1$年月日 <- as.Date(nextMonth - 3600*24)

別解

見直して、コードの見通しを改善しました。

tmpDate <- as.POSIXlt(gsub("([0-9]+)/([0-9]+)", "\\1/\\2/1", df1$年月))
tmpDate$mon <- tmpDate$mon + 1 # 1ヶ月ずらす（桁上がり処理はされる）
tmpDate$mday <- 0 # 翌月の0日目は、当月の月末
df1$年月日 <- as.Date(tmpDate)

*1:正確には因子になります。

*2:文字列として2013/2と2013/11を比較すると、2013/11のほうが小さくなります。2013/02としてあれば良いのですが。

*3:必ず1日です。

Excelでもプログラミングができる事を忘れた経済学徒へ

Excel/VBAで大量のワークシートを一括してCSVで保存できます。
とりあえずコードだけ。Excelブック内にマクロを置く/書く方法は「Excel 2010 VBA の基礎知識」（Excel for Mac 2011）などを参照してください。

Sub J_YAMASAKI()
For Each mySheet In Worksheets
mySheet.Activate
' 保存先ディレクトリは C:\ を ~/J_YAMASAKI のように適当に変えてお使いください
ActiveWorkbook.SaveAs Filename:="C:\" & mySheet.Name & ".csv", FileFormat:=xlCSV, _
CreateBackup:=False
Next
End Sub

パネルデータで全員が一斉に説明変数の値を変化させたときのタイムダミーの係数

立命館大学の柴田悠氏への私信なのですが、パネルデータ分析の固定効果モデルに年次などタイムダミーが入っているときに、ある瞬間に個々が同じような行動をとって、説明変数の値を一斉に変化させたときに、それがタイムダミーの係数として観測されない事を、シミュレーションで示したいと思います*1。

1. モデル

計量モデルは以下になります。

Yが被説明変数、Xが説明変数、aが固定効果、βとγは推定する係数、Iが個々の数、iが個々を表す添字、Tが期間の長さ、tが期を表す添字とします。εは誤差項です。

2. 係数の真の値

Iは10、Tは5として、真の値はβが0.015、が{0.00 0.05 0.04 0.06 0.02}、が{0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0}を設定します。

3. 観測値の生成

観測値になるXは一様分布から乱数で0から1を生成し、t=3のときだけ+1するようにしましょう。ある瞬間に個々が同じような行動をとった例とします。誤差項εは標準偏差0.1の正規分布から生成します。Xとεが決まれば、真の値から観測値Yも定まります。
Rで生成するためのコードは以下になります。

set.seed(201408)
I <- 10 # 個体の数
ai <- (1:i)/10 # 固定効果
T <- 5 # 期間の長さ
gamma <- c(0, (5^(1:(T-1)) %% 7)/100) # タイムダミーの効果
epsilin <- rnorm(I*T, sd=0.1)
df <- data.frame(
  i = numeric(I*T), t = numeric(I*T), Y = numeric(I*T), X = numeric(I*T)
)
for(i in 1:I){
  for(t in 1:T){
    l <- (i-1)*T + t
    df$i[l] <- i
    df$t[l] <- t
    df$X[l] <- runif(1) + ifelse(t==3, 1, 0)
    df$Y[l] <- ai[m] + 0.15*df$X[l] + gamma[t] + epsilin[l]
  }
}

生成した観測値の一部を見ると、こうなります。t=3のときに、明らかにXが大きくなっていることを確認してください。

i	t	Y	X
1	1	1.0242424	0.90365560
1	2	1.2447202	0.74466442
1	3	1.2130497	1.03975109
1	4	1.3497088	0.29219997
1	5	1.0248503	0.02165759
2	1	1.3007814	0.63130932
2	2	1.3448006	0.86396715
2	3	1.2383986	1.17330402
2	4	1.2283682	0.66754810
2	5	1.1475519	0.75067122

4. 推定結果

ちゃっちゃと固定効果モデルで推定してみましょう。plmパッケージを使います。

library(plm)
plmdata <- plm.data(df, index=c("i", "t"))
td <- as.factor(df$t)
rfe <- plm(Y ~ X + td, model="within", data=plmdata)
summary(rfe)

推定結果は以下になります。

Oneway (individual) effect Within Model

Call:
plm(formula = Y ~ X + td, data = plmdata, model = "within")

Balanced Panel: n=10, T=5, N=50

Residuals :
Min. 1st Qu. Median 3rd Qu. Max.

• 0.16200 -0.05120 -0.00315 0.04550 0.16500

Coefficients :
Estimate Std. Error t-value Pr(>|t|)
X 0.188583 0.049956 3.7750 0.0005953 ***
td2 0.067277 0.041042 1.6392 0.1101244
td3 -0.015109 0.059223 -0.2551 0.8001284
td4 0.113756 0.040291 2.8233 0.0077890 **
td5 0.043061 0.040308 1.0683 0.2926920

• • -

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Total Sum of Squares: 0.54784
Residual Sum of Squares: 0.284
R-Squared : 0.4816
Adj. R-Squared : 0.33712
F-statistic: 6.50321 on 5 and 35 DF, p-value: 0.00022576

Xが0.188583と推定されている一方で、t=3のタイムダミーの係数は-0.015109となっています。観測数が十分ではないのか精度に欠けますが、タイムダミーの値は過少に推定されていますから、タイムダミーの係数として観測されない事が分かります。
また、t=3のインパクトを大きくとっても、推定結果が大きく変わることはありません。観測数を十分増やすと、推定値は真の値に近づきます。この例ではI=300ぐらいにすると、Xの係数βが0.1541469になりました*2。

*1:数理的には説明変数とタイムダミーの共分散がゼロである限りは、十分なサンプルサイズで推定結果に影響を及ぼさないことは、ほぼ自明です。

*2:係数の割りには分散が大きすぎたかも知れません。

統計モデルに観測値と観測値の割り算値を入れたときのバイアス

「データ解析のための統計モデリング入門」の著者の久保拓弥氏へのお返事なのですが、別所の「統計モデルに観測値と観測値の割り算値を入れても問題ない」に対して以下のようなコメントをもらったので、具体的な例を作ってみました*1。

…まあ，みなさん割算値だい好きだし，これからも割算値いりの統計モデルが使われるのでしょう．とりあえず「この場合は明らかにかなりまずいでしょ」とわかる例を何か作ってみようかな…

誤差項がコーシー分布のようなものになったときに、どのぐらいバイアスがかかるのかに関して、直観的な話です。

1. 真のモデルに割り算が無いケースを考える

以下のようなx、y、zの関係を現す真のモデルを考えます。

「観測値は非確率変数で、未知の何かが誤差項を作っている」と仮定すると終了するので、xの観測値x'はxと正規分布に従う観測誤差、yの観測値y'はと正規分布に従う観測誤差の合算とします。後のシミュレーションでパラメーターを減らすために、xとyの観測誤差はi.i.dとします。
変形してみましょう。

単純に推定すると1/yの影響を忘れてかなり大きな誤差が出ます。x/yがモデルに入るときは、1/yの影響が無い事が理論的に演繹されている気もしますが、今回は特定化バイアスではなく誤差の分布の影響を比較するために残します。
推定モデルを整理しておきます。εとηは誤差項です。
割り算なし：
割り算あり：
一様分布からxとyを作り出しzを計算して、xとyに誤差項を加えてx'とy'を作ってから、x'、y'、zでデータセットを作成し、そこからの推定量を計算していきます。真の値は2です。
さて、割り算なしと割り算ありの違いを見てみましょう。

観測値の誤差が小さい場合は差は目立ちませんが、誤差が大きくなると割り算ありモデルの推定結果が不安定になります。「この場合は明らかにかなりまずいでしょ」とわかる例に思えるかも知れませんが、実は説明力を失って、真の値から乖離している領域であることに注意してください。なお測定誤差が大きくなると、切片項以外の推定される係数はゼロに近づきます。

なお割り算ありモデルの残差にシャピロ-ウィルク検定をかけると、ほぼ正規分布にならない事が分かります。一方で、割り算なしモデルの残差はほとんど正規分布していました。無理に割り算を入れるのは、よした方が良いようです。

2. 真のモデルに割り算があるケースを考える

以下のようなx、y、zの関係を現す真のモデルを考えます。

xとyの観測値の誤差は正規分布だと考えるので、x/yの観測誤差の分布はコーシー分布になります。
推定モデルを整理しておきます。
割り算なし：
割り算あり：

これも「この場合は明らかにかなりまずいでしょ」とわかる例に思えるかも知れませんが、ある程度は信頼のおける推定値である青点線の左側では、割り算のありなしで大差は見られません。
なお、こちらの推定の残差にシャピロ-ウィルク検定をかけると、どちらもほとんど正規分布ではないことになります。割り算ありモデルは割り算で、割り算なしモデルは掛け算で分布が歪んでしまうようです。

2.1 本当にヤバいぐらい壊れるケース

後から気づいたので追記します。setup関数内のxとyの初期値を以下にして、第2節のグラフを描くと以下のように割り算で派手に壊れます。

x <- rnorm(n, sd=5) # xの真の値（0にかかる正規分布）
y <- rnorm(n, sd=5) # yの真の値（0にかかる正規分布）

何が起きたのかと思っていたのですが、偶発的に異常値がx/yにできるので、それに推定結果が引っ張られてしまったようです。以下がループ中で推定値が飛んだとき（setupの引数がsd=0.03）のヒストグラム。

(；ﾟдﾟ) -200以下と、+100以上！？
xとyの真の値の分布がrnorm(n, sd=5) + 30だったりすると問題が出ないので、常に問題になるわけではないですが、x/yの分布図は見ておいたほうが無難みたいです。

3. モデルの特定化の方が大事に思える

誤差の大きさや特定化の精度の程度によりますが、割り算による影響が大きいとは限りません。どこかの演習問題でx/yの誤差の分布は正規分布で近似できるとありましたが、ある程度はそういう性質があるようです。
少なくとも観測値が非確率的と見なせるほど精度が高ければ気にしなくて良いですし、質的選択モデルのような計量モデルの都合で割り算を排除できないときに、観測値と観測値の割り算をためらう理由も無い気がします。心配性の人は、残差の分布を確認しましょう。
割り算を排除したとしても、それによってモデルの特定化に失敗していたら、誤差は大きくなります。変数をかけたり*2、対数をとったりしても誤差の分布は歪むわけです。現実的に完璧な推定はあり得ませんから、力の入れどころは考えていく必要があると思います。

A. ソースコード

上のグラフ二枚のプロットに使ったコードは以下になります。

#
# n: 観測数, sd: 標準偏差, hg: 不均一分散(TRUE/FALSE)
# model: 真のモデルの数式表記
# return: x, y, zの観測値
#
setup <- function(n=100, sd=1, hg=FALSE, model=parse(text="1+2*x-3*y")){
  x <- runif(n, 1, 3) # xの真の値
  y <- runif(n, 1, 2) # yの真の値
  u <- rnorm(n, sd=sd) # yの観測誤差
  oy <- y + u # yの観測値
  e <- rnorm(n, sd=sd) # xの観測誤差
  # 不均一分散のときは上書き
  if(hg){
    for(i in 1:n){
      e[i] <- rnorm(1, sd=max(1e-6, sd*y[i])) # 標準偏差は0より僅かに正にする
    }
  }
  ox <- x + e # xの観測値
  # 被説明変数zは真の値に従う
  z <- eval(model)
  data.frame(x = ox, y = oy, z=z)
}


#
# シミュレーションで比較してプロット
# n: 観測数, min_sd: 標準偏差の最小値, max_sd: 標準偏差の最大値
# hg: TRUEならば不均一分散を入れる（未使用）
# model: 真のモデルのテキスト表記
# plegend: 凡例の位置
#
compare <- function(n=100, min_sd=1e-06, max_sd=1, hg=FALSE, model="1+2*x-3*y", plegend="topright"){
  len <- 100
  compared <- data.frame(sd=numeric(len), non_divided=numeric(len), divided=numeric(len), nd_sw_test=numeric(len), d_sw_test=numeric(len), t_test=integer(len))
  compared$sd <- seq(max(1e-06, min_sd), max_sd, length.out=len)
  for(i in 1:len){
    df <- setup(n=n, sd=compared$sd[i], hg=hg, model=parse(text=model))
    # ベタベタな分岐
    if(model=="1+2*x-3*y"){
      # 普通に推定
      r <- lm(z ~ x + y, data=df)
      # 割り算推定
      z_p_oy <- df$z/df$y
      x_p_oy <- df$x/df$y
      c_p_oy <- 1/df$y
      r_p_oy <- lm(z_p_oy ~ x_p_oy + c_p_oy)
    }else{
      # 割り算あり
      yz = df$z*df$y
      r <- lm(yz ~ y + x + 0, data=df)
      # 割り算なし
      x_p_oy <- df$x/df$y
      r_p_oy <- lm(df$z ~ x_p_oy)
    }
    # 切片項
    compared$non_divided[i] <- coef(r)[2]
    compared$divided[i] <- coef(r_p_oy)[2]
    # 正規性の検定結果
    compared$nd_sw_test[i] <- shapiro.test(residuals(r))$p.value
    compared$d_sw_test[i] <- shapiro.test(residuals(r_p_oy))$p.value
    # 95%信頼区間に2.0が含まれるか
    compared$t_test[i] <- ifelse(abs(2.0 - coef(r)[2])<coef(summary(r))[, 2][2]*qt(1-0.05/2, r$df.residual), 1, 0)
  }
#  ylim <- c(min(compared$non_divided, compared$divided), max(compared$non_divided, compared$divided))
  ylim <- c(0, 4)
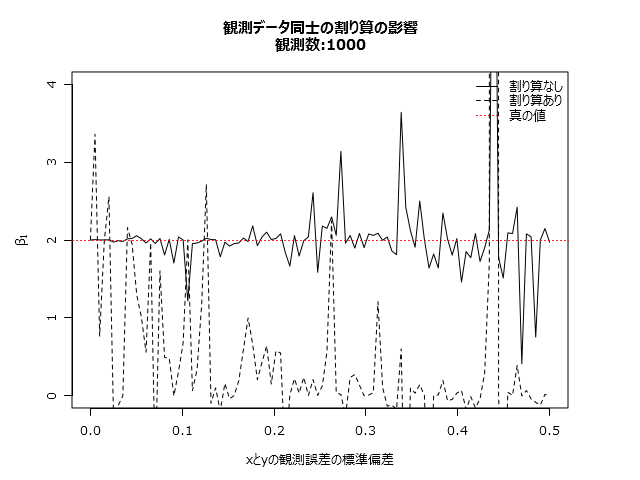
  plot(non_divided ~ sd, data=compared, xlim=c(min_sd, max_sd), ylim=ylim, type="l", main=sprintf("観測データ同士の割り算の影響\n観測数:%d%s", n, ifelse(hg,"，不均一分散あり","")), xlab=sprintf("xとyの観測誤差の標準偏差%s", ifelse(hg, "(y=1のとき)", "")), ylab=parse(text = "beta[1]"))
  lines(compared$sd, compared$divided, lty=2)
  abline(h=2, col="red", lty=3)
  # ある程度の信頼性の推定値を出した最大の標準偏差
  rsd <- max(subset(compared, t_test==1)$sd)
  abline(v=rsd, col="blue", lty=4)
  text(rsd, 0, "推定値の95%信頼区間に2が入る限界線", col="blue", adj=c(0, 0))
  legend(plegend, lty=c(1, 2, 3), pch=-1, legend=c("割り算なし", "割り算あり", "真の値"), col=c("black","black","red"), bty="n")
  return(compared)
}


# 第1節のグラフ
set.seed(201408)
rd <- compare(max_sd=0.5, n=1000)


# 第2節のグラフ
set.seed(201408)
rd <- compare(max_sd=0.5, n=1000, model="1+2*(x/y)")

B. 不均一分散

こうすると不均一分散があるときに、割り算があるときのほうが、マシな推定量になる事が分かります。まぁ、クマが体長10cmから50mまであったりしないでしょうから、社会科学系のデータでないと気にする必要はないかも知れませんが。

set.seed(201408)
rd <- compare(max_sd=0.5, n=1000, hg=TRUE)

*1:ソースコードは公開するので、ミスがあったときは御勘弁を

*2:第2種の変形されたベッセル関数になるそうです。残念ながら、モーメント母関数などを持つかは確認していません。