OpenBLASをリンクしたWindows版R 4.1 PR

ループでスカラ演算を繰り返すよりもベクトル演算をした方が速いRですが、標準構成ではNetlib BLASと言う線形代数ライブラリBLASのリファレンス実装を使っていて、行列演算、ベクトル演算も速いとは言えないものとなっています。チューニングされたOpenBLASに差し替えることで、高速化をしてみましょう。

Ubuntu Linuxでは、

sudo apt install libopenblas0-pthread

で、OpenBLASがインストールされ、aptでインストールしたRはOpenBLASを使うようになります。簡単ですね。しかし、Windowsだと時間のかかる作業が必要です。
基本的にはチートペーパーを見ながら、Rの開発版をコンパイルできる環境を揃えて、ビルドに使う設定ファイルを書き換えれば終わりなのですが、微妙に書いてある通りではコンパイルできませんでした。

まず、Step 4: Create blas patchのところですが、現行のMakefile.winがホワイトスペースに空白ではなくタブを使っているせいか、示されているblas.diffではパッチがあたりません。blas.diffをつくりなおす必要がありました。作り直したblas.diffをr-base-master.zipを展開してできるフォルダーC:\r-base-masterの中に入れました。

次に、Step 5: Adjust existing filesのところですが、示されているPKGBUILDの末尾の</jeroen@berkeley.edu>は要らないので消しました。見比べるとmakedependsに"${MINGW_PACKAGE_PREFIX}-openblas"、sourceにblas.diff、sha256sumsに'SKIP'、# Add your patches hereにpatch -Np1 -i "${srcdir}/blas.diff"をそれぞれ追加しているだけのようなので、チートペーパーのPKGBUILDをコピペする必要は無いかもです。（これはチートペーパーに記述の問題はありませんが）MkRules.local.inのQPDFへのパスは、

QPDF = C:/qpdf-10.0.1

と、インストール先のQPDFのホームにしました。
export PATH="$PATH:/c/progra~1/MiKTeX 2.9/miktex/bin/x64"の行は、

export PATH="$PATH:/c/progra~1/MikTeX/miktex/bin/x64"

と、（自明ですが）MikTeXのインストール先にあわせました。

設定は以上で終わりですが、別のチートペーパーを参考にビルドする前にMikTeXでフォントを作成しておかないとFont ts1-zi4r at 540 not foundとエラーが出て止まります*1。

Step 6: Build Rはマイナーなところですが、rtools40のmsys.exeを使えと書いてありますが、手元の環境ではC:\rtools40\msys2.exeでした。
なお、コンパイル途中でQPDFがインストール確認をしてくるので、少なくとも1回は了解ボタンを押すまでは、放置しておいてもコンパイルは終了しません。また、マイナーな計算結果差のようですが、微妙に1つのテストでエラーが出ました。これは4.1 PRのせいかも知れません*2。

コンパイルが終わってR-devel-win.exeができたらすぐにインストールしてみたのですが、Windows版ではsessionInfo()をしても使っているBLASの種類を教えてくれないです。以下のように行列演算をさせ、4コアCPUで35倍以上の経過時間差を出して、差し替えた感を実感しました。

set.seed(1013)
n <- 5000
M1 <- matrix(runif(n^2, min=1, max=10), n, n)
M2 <- matrix(runif(n^2, min=1, max=10), n, n)
system.time({ M3 <- M1 %*% M2 })

ところで先日書いてみたマクロ経済学の数値解析は、ほとんど速くなりませんでした。速くなりませんでした。

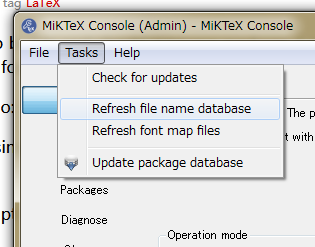
*1:チートペーパーのコマンドをうってinitexmf: security risk: running with elevated privilegesとエラーが出る人は、付属ユーティリティMiKTeX Consoleで操作した方がよいかもです。起動してadministration modeを選択し、メニューのTasksのRefresh file name database、Refresh font map filesを順番に実行します。

*2:export rsource_url='https://cran.r-project.org/src/base-prerelease/R-latest.tar.gz'; ./full-build.shとコンパイルを実行すると、開発版ではなくリリース候補版のソースコードを指定できます。

Rの拡張でOpenMPを使ってみる

プロセッサのマルチコア化が進んだ現代なので、時間のかかる計算では並列処理をするコードを書くのが望ましいです。スレッドやセマフォの制御を直接プログラミングすると骨が折れるのですが、シングルコア向け逐次処理コードを並列処理に変換してくれるOpenMPという仕組みがあります。Cで書いたRの拡張で使ってみましょう。

1. Makevarsの編集

gccでOpenMPを使うためには、引数に-fopenmpフラグを加える必要があります。R CMDでこの引数をつけるためには、LinuxやMacOS Xでは$HOME/.R/Makevarsに、MS-Windowsでは%HOME%*1/.R/Makevars.winと言うテキストファイルに、

CFLAGS= -fopenmp
CXXFLAGS= -fopenmp
# PKG_CXXFLAGSか、PKG_CXXFLAGSに-std=c++11と書いてCXX11FLAGSに-fopenmpをつける（C++14/17でも同様）ほうがよいときもあります。

と言うようにかいておきます。なお、-O3オプションなども同様につきます。

2. Cのソースコードの編集

ループされていて一定以上の処理時間がかかるコードの例として、2つの一行を除けば同じ（無意味な）関数をOMPexample.cとして保存します。

#include<R.h>
#include<Rinternals.h>

SEXP example(SEXP m){
  int i, j, n;
  double s1 = 0, s2 = 0;
  int nor, noc;
  SEXP rv, dim;

  /* 第一引数が行列か確認 */
  if(!isMatrix(m))
    error("A matrix is required for the first argument.");

  /* 行列の行数、列数を得る */
  dim = getAttrib(m, R_DimSymbol);
  nor = INTEGER(dim)[0]; /* 行数 */
  noc = INTEGER(dim)[1]; /* 列数 */

  for(j=0;j<noc;j++){
    for(i=0;i<nor;i++){
      s1 += REAL(m)[i+j*nor]*(i+1)/(j+1); /* 行列と言っても一次元配列 */
      s2 -= REAL(m)[i+j*nor]*(i+1)/(j+1);
    }
  }

  rv = PROTECT(allocVector(REALSXP, 2));
  REAL(rv)[0] = s1;
  REAL(rv)[1] = s2;
  UNPROTECT(1);

  return rv;
}

SEXP OMPexample(SEXP m){
  int i, j, n;
  double s1 = 0, s2 = 0;
  int nor, noc;
  SEXP rv, dim;

  /* 第一引数が行列か確認 */
  if(!isMatrix(m))
    error("A matrix is required for the first argument.");

  /* 行列の行数、列数を得る */
  dim = getAttrib(m, R_DimSymbol);
  nor = INTEGER(dim)[0]; /* 行数 */
  noc = INTEGER(dim)[1]; /* 列数 */

  #pragma omp parallel for private(i, j) reduction(+:s1) reduction(-:s2)
  for(j=0;j<noc;j++){
    for(i=0;i<nor;i++){
      s1 += REAL(m)[i+j*nor]*(i+1)/(j+1); /* 行列と言っても一次元配列 */
      s2 -= REAL(m)[i+j*nor]*(i+1)/(j+1);
    }
  }

  rv = PROTECT(allocVector(REALSXP, 2));
  REAL(rv)[0] = s1;
  REAL(rv)[1] = s2;
  UNPROTECT(1);

  return rv;
}

大学の情報基盤センターなるところが書いたネット上にあるOpenMPの解説を読めばすぐ分かりますが、プリプロセッサ命令

  #pragma omp parallel for private(i, j) reduction(+:s1) reduction(-:s2)

がOpenMPの記述になります。private(i, j)は並列処理で変数iとjは、それぞれ異なる値をシェアしない変数として扱うことを意味し、reduction(+:s1)は、それぞれの並列処理で加算されていくそれぞれの変数s1は、並列処理の終了時に一つに合算されることを意味します。reduction(-:s2)は、加算ではなく減算処理をあわせます。
なお、OpenMPが有効でない場合は、このプリプロセッサは無視されて逐次処理されるコードが出力されます。

3. Cのソースコードをコンパイルする

OMPexample.cを用意したら、以下のようにすると、OMPexample.so（もしくはOMPexample.dll）と言うRの拡張が出来上がります。

R CMD SHLIB OMPexample.c

Rtoolsが入っていないと動かないので注意してください。

4. Rから拡張を呼び出して使う

OpenMPを使ったOMPexample関数と、使っていないexample関数の速度比較をRでしてみましょう。

dll <- dyn.load(paste("OMPexample", .Platform$dynlib.ext, sep = ""))
example <- function(m) .Call("example", m)
OMPexample <- function(m) .Call("OMPexample", m)

set.seed(1002)
n <- 5000 # 一瞬で処理が終わる人は増やすと時間をかけられます
m <- matrix(rnorm(n*n), n, n)

print(system.time({
  cat("No OpenMP: ", example(m), "\n")
}))

print(system.time({
  cat("OpenMP: ", OMPexample(m), "\n")
}))

搭載されているプロセッサ数に応じて速くなります。並列化と言っても、手軽に試せますね。

A. Rcpp/Eigen

Rcppの行列はスレッドセーフではないのでOpenMPの並行処理の中で使えませんが、Eigenは最初にEigen::initParallel();をして行列をスレッドセーフにしておくだけで、OpenMPの並列処理の中で行列を使うことができます。つまり、Rcppの行列からEigenの行列を作成して処理を行うことで、RcppからOpenMPを使うことができます。RcppPararellを使うべきと思うかも知れませんが、RcppPararellはWorkerクラスを定義しないといけないので記述が煩雑な一方、Eigen/OpenMPと比較して速度的なアドバンテージはほぼ無いようです。

*1:OSで用意される環境変数ではないので、Rで Sys.getenv("HOME") をして確認してください。

疎な巨大対称行列の一般化固有値問題のC++/Eigenでの効率的な解き方

「水素原子に対するSchrödinger方程式を有限要素法で数値的に解いてみる（C++のソースコード付き）」で紹介されているC++/Eigenのコードを、（ページ著者が）Juliaに移植してみたら12倍くらい速くなったと言うツイートが流れてきて、気になってC++の方のソースコードを見てみたのですが、

• 巨大な疎行列であること
• 必要な固有値が1つであること*1

を活かしておらず、この2点を利用すればもっと時間を短縮できるものでした*2。実際、そう大きくない変更で、手元の環境では25分の1の時間で計算が終わるようになりました。

追記(2021/02/15 01:42):ブログ主が、有限要素法による水素原子のエネルギー固有値が、小さい方から見てどこまで正確かを検証する部分を加筆しました（図1, 図2）。これによって行列の固有値がすべて必要になるので、以下の方法は適切な計算方法にならないです。

なお、すべての固有値を得る場合にJulia比較でC++/Eigenが遅いのは、どうもC++/Eigenが自動的に並列化してマルチコアを活かしてこないところにあるので、その辺を何らかの方法*3で解消すると高速化できます。

EigenはC++用の線形代数ライブラリなのですが、名前がEigenなのに疎行列（Sparse Matrix）用の固有値問題のソルバーが無かったりします。上述のコードでは、GeneralizedSelfAdjointEigenSolverと言う計算する行列式に、疎行列、対称、正定値と言った条件を使わない上に、行列の固有値をすべて用いようとするソルバーが用いられています。汎用ソルバーとしても遅いというような指摘もあるようですが、入力データの特性を活かすのは高速化のイロハです。

この手の数値演算アルゴリズムを実装しようとすると数学の理解やデバッグの手間隙に大変な労力を費やすことになりますが、幸い、手軽に使えるテンプレート・ライブラリでSpectraと言うのがあります。具体的には、一般化固有値問題の計算対象の2つの行列をEigen::SparseMatrixで持ち、SymGEigsSolverと言うソルバーと解きます。なお、使ってみると癖があるなと思う部分があって、特にコンストラクタの第4引数を小さく取りすぎると固有値が収束しなかったとエラーを出して来るところには注意が必要です。

差分は以下になります。コンパイル時にダウンロードして展開したSpectraへインクルード・パスを通さないとコンパイル・エラーになるので気をつけてください。

--- a/src/hydrogen_fem/hydrogen_fem.cpp
+++ b/src/hydrogen_fem/hydrogen_fem.cpp
@@ -12,19 +12,24 @@
#include <memory> // for std::unique_ptr
#include <boost/assert.hpp> // for BOOST_ASSERT
#include <Eigen/Eigenvalues> // for Eigen::GeneralizedSelfAdjointEigenSolver

+#include <Eigen/Sparse>
+#include <Spectra/SymGEigsSolver.h>
+#include <Spectra/MatOp/SparseGenMatProd.h>
+#include <Spectra/MatOp/SparseCholesky.h>
+#include <iostream>
namespace hydrogen_fem {
// #region コンストラクタ

Hydrogen_FEM::Hydrogen_FEM()
- : hg_(Eigen::MatrixXd::Zero(NODE_TOTAL, NODE_TOTAL)),
+ : hg_(Eigen::SparseMatrix<double>(NODE_TOTAL, NODE_TOTAL)),
length_(ELE_TOTAL),
mat_A_ele_(boost::extents[ELE_TOTAL][2][2]),
mat_B_ele_(boost::extents[ELE_TOTAL][2][2]),
nod_num_seg_(boost::extents[ELE_TOTAL][2]),
node_r_ele_(boost::extents[ELE_TOTAL][2]),
node_r_glo_(NODE_TOTAL),
- ug_(Eigen::MatrixXd::Zero(NODE_TOTAL, NODE_TOTAL))
+ ug_(Eigen::SparseMatrix<double>(NODE_TOTAL, NODE_TOTAL))
{
}

@@ -42,20 +47,33 @@ namespace hydrogen_fem {

// 全体行列を生成
make_global_matrix();

// 一般化固有値問題を解く
- Eigen::GeneralizedSelfAdjointEigenSolver<Eigen::MatrixXd> es(hg_, ug_);

+  Spectra::SparseSymMatProd<double> Aop(hg_);
+  Spectra::SparseCholesky<double> Bop(ug_);
+
+  // 第3引数の1は要求する固有値の数，第4引数は収束速度（とメモリー利用量と行列操作の複雑さ）を定める値
+  Spectra::SymGEigsSolver<double, Spectra::SMALLEST_ALGE, Spectra::SparseSymMatProd<double>, Spectra::SparseCholesky<double>, Spectra::GEIGS_CHOLESKY> geigs(&Aop, &Bop, 1, NODE_TOTAL<10 ? NODE_TOTAL : 10 + (NODE_TOTAL - 10)/100);
+
+  geigs.init();
+  int nconv = geigs.compute();
+  if(Spectra::SUCCESSFUL != geigs.info()){
+    std::cerr << "geigs.info(): " << geigs.info() << std::endl;
+    exit(-1);
+  }

// エネルギー固有値Eを取得
- auto const e = es.eigenvalues()[0];
+ Eigen::VectorXcd evalues = geigs.eigenvalues();
+ auto const e = evalues[0].real(); // 計算結果は複素数なことに注意．なお、複数の固有値を求めた場合、なぜか小さい順に固有値が並んでいるわけではない.

// 固有ベクトル（波動関数）を取得
- phi_ = es.eigenvectors().col(0);
+ phi_ = geigs.eigenvectors(1).col(0).real(); // なぜか添字が1からなのと、計算結果は複素数なのに注意

// 固有ベクトル（波動関数）を規格化
normalize();

return e;
}

void Hydrogen_FEM::save_result() const
@@ -190,8 +208,8 @@ namespace hydrogen_fem {
for (auto e = 0; e < ELE_TOTAL; e++) {
for (auto i = 0; i < 2; i++) {
for (auto j = 0; j < 2; j++) {
- hg_(nod_num_seg_[e][i], nod_num_seg_[e][j]) += mat_A_ele_[e][i][j];
- ug_(nod_num_seg_[e][i], nod_num_seg_[e][j]) += mat_B_ele_[e][i][j];
+ hg_.coeffRef(nod_num_seg_[e][i], nod_num_seg_[e][j]) += mat_A_ele_[e][i][j];
+ ug_.coeffRef(nod_num_seg_[e][i], nod_num_seg_[e][j]) += mat_B_ele_[e][i][j];
}
}
}

--- a/src/hydrogen_fem/hydrogen_fem.h
+++ b/src/hydrogen_fem/hydrogen_fem.h
@@ -15,6 +15,9 @@
#include <Eigen/Core> // for Eigen::MatrixXd
#include <boost/multi_array.hpp> // for boost::multi_array

+#include <Eigen/Core>
+#include <Eigen/SparseCore>
+
namespace hydrogen_fem {
//! A class.
/*!
@@ -144,7 +147,7 @@ namespace hydrogen_fem {
/*!
左辺の全体行列
*/
- Eigen::MatrixXd hg_;
+ Eigen::SparseMatrix<double> hg_;

//! A private member variable.
/*!
@@ -192,7 +195,7 @@ namespace hydrogen_fem {
/*!
右辺の全体行列
*/
- Eigen::MatrixXd ug_;
+ Eigen::SparseMatrix<double> ug_;

// #region 禁止されたコンストラクタ・メンバ関数

*1:すべての固有値を取りたい場合もあるわけですが、大学のレジュメなどを拝見する限りは、最小値か最大値のどちらか一つを計算すれば間に合うケースが多いようです。

*2:最初からすべて分かったように書いていますが、ページ著者と試行錯誤して、この結論にたどり着いています。

*3:OpenBlASを使う方法が紹介されていました。

FASTGLを使ってC++で積分

数値解析における数値積分法の代表としてガウス求積と言う技法があり、それに必要なガウス点と重みの計算でJuliaがC++より桁違いに速いと言う話が流れていたのですが、Juliaで使われているFastGaussQuadrature.jlが使っているアルゴリズムのC++版を使ったところ、案の定、だいたい同じの速度になりました。

Fast computation of Gauss-Legendre Quadrature Points and Weights（FASTGL）のアルゴリズム開発者のページからfastgl.cppとfastgl.hppをダウンロードしてきて、積分に使うだけです。サブディレクトリfastglにこの2つのファイルを配置したところで、以下のソースコードのファイルを作成してコンパイルしたら簡単に実行できます。-O3 -lmオプションはいると思いますが。

#include <iostream>
#include <chrono>
#include <iomanip>
#include <functional>
#include "fastgl/fastgl.hpp"

/*
  FASTGLを使って積分をする関数
  args: ラムダ関数f(x), xの最小値, xの最大値, 節点の数
*/
double integral(std::function<double(double)> f, double s, double e, int NumberOfKnots){
  double Res = 0.0;
  double xm = 0.5 * (s + e);
  double xr = 0.5 * (e - s);

  for ( int k = 1 ; k <= NumberOfKnots ; ++k ){
    fastgl::QuadPair p = fastgl::GLPair ( NumberOfKnots, k );
    Res += p.weight * f( xm + xr * p.x());
  }

  return Res*xr;
}

int main(){
  std::chrono::system_clock::time_point stime, etime;
  stime = std::chrono::system_clock::now();

  // boost::math::quadratureあたりと異なり、節点が100万個でも大した時間にならない
  double Res = integral([](const double& t) { return 1.0 / 2 / std::sqrt(t); }, 1, 4, 1000000);

  etime = std::chrono::system_clock::now();

  std::cout << std::setprecision(16);
  std::cout << "Results: " << Res << std::endl;
  std::cout << "Elapsted Time: " << std::chrono::duration_cast<std::chrono::milliseconds>(etime - stime).count() << " ms" << std::endl;

  return 0;
}

モンテカルロ法で円周率を計算するベンチマーク

モンテカルロ法で円周率を計算するベンチマークで、Juliaと比較してgccが悪い言われているのですが、本当なのか検証してみましょう。

CとJuliaでこの分岐が単純なマイクロベンチマークを実行すると、乱数生成の速度が結果を大きく左右しえます。後方互換性の問題で、Cの標準の乱数生成関数は線形合同法になっています。Juliaの方は標準がdouble precision SIMD oriented Fast Mersenne Twister pseudorandom number generator (dSFMT)で、明示的にMersenneTwisterを使った場合もdSFMTを用いているようです。Cの方もdSFMTを用いてベンチマークを取ることにします。

Cのソースコード

dSFMTがよくチューニングされているので、私には工夫の余地は無く、オーソドックスに書いています。なお、生成した実行ファイルをreadelfで調べたところ、dSFMTがヘッダーファイルでinline static宣言している関数はインライン展開されていました。10回計測して、一番短い経過時間を採用しています。

#include <time.h>
#include <stdlib.h>
#include <stdio.h>
#include <limits.h>
#include "dSFMT.h"
#include <float.h>
#include <math.h>

/*
dSFMT-src-2.2.3.tgz を展開したディレクトリで、ソースコードのファイル名をpi_mc_dsfmt.cとして、

clang -o pi_mc pi_mc_dsfmt.c dSFMT-src-2.2.3/dSFMT.c -IdSFMT-src-2.2.3/ -DDSFMT_MEXP=521 -msse2 -DHAVE_SSE2 -O3 -lm

とコンパイルしました。gccとclangはオプションが同じなので、gccとの比較は容易に行えます。
*/

double pi_mc(long n_iter) {
  double  x, y;
  dsfmt_t rng;

  dsfmt_init_gen_rand(&rng, time(NULL));

  int n_in = 0;
  for (long i = 1; i <= n_iter; i++) {

    x = dsfmt_genrand_open_open(&rng);
    y = dsfmt_genrand_open_open(&rng);

    if (x * x + y * y < 1.0)
      n_in++;
  }

  return (double)4.0*n_in/n_iter;
}

int main(){
  struct timespec t1, t2;
  double  dt, sum_dt, min_dt;
  double  r = 0;
  size_t  n;
  int  j, nos = 10;

  printf("log10(n)\telapsed time (seconds)\n");

  for(n=1; n<=1000000*1000; n*=10){
    sum_dt = 0;
    min_dt = DBL_MAX;
    for(j=0; j<nos; j++){
      clock_gettime(CLOCK_THREAD_CPUTIME_ID, &t1); // clock()を使って計測しても、ほぼ同じ数字になります

      r = pi_mc(n);

      clock_gettime(CLOCK_THREAD_CPUTIME_ID, &t2);

//      fprintf(stderr, "estimated pi: %f\n", r);

      dt = (double)(t2.tv_sec - t1.tv_sec) + (double)(t2.tv_nsec - t1.tv_nsec)/1000000000;
      
      sum_dt += dt;
      if(min_dt > dt)
        min_dt = dt;
    }

    printf("%.0f\t%.09f\n", log10(n), min_dt);
  }

  return 0;  
}

Juliaのスクリプト

Cのとだいたい同じですが、グローバル変数へのアクセスが無いように一番外側ループ部分も関数内にしまいました。

using Random
# using Random: default_rng

function pi_mc(n_iter)
n_in = 0
# rng = default_rng()
rng = MersenneTwister(time_ns())
for i in 1:n_iter
x, y = rand(rng), rand(rng)
n_in += ifelse(x^2 + y^2 ≤ 1, 1, 0)
end
4n_in/n_iter
end

function loop(s, e)
  n = s
  while(n <= e)
    sum_dt = 0;
    min_dt = 3600;
    for i in 1:10
      t1 = time_ns()
      r = pi_mc(n)
      t2 = time_ns()
      dt = (t2 - t1)/1000000000
      sum_dt = sum_dt + dt
      if(min_dt > dt)
        min_dt = dt
      end
#      println("estimated pi: ", r)
    end
    println(log10(n), "\t", min_dt)
    n = n*10
  end
end

println("log10(n)", "\t", "elapsed time (seconds)")

loop(1, 10^9)

SIMD拡張命令セットでgcc用のsum関数を書いてみる

とあるJuliaを使った教材に、JuliaやNumPyのsumはSIMD拡張命令セットを使うから速いけれども、C言語でsumを書くとそうではないから遅いような記述があって、CからSIMDを叩けば良いだろうと思ったので、私にしては珍しくC99のコードで、単浮動小数点のsumを書いてみました。gccでしかコンパイルできません。

謳い文句によるとgccは自動的にSIMD拡張命令セットを使うことになっていますが、実際のところはsumのような単純なものでも使いません。こんなにSIMD向きの単純計算でも、128bitsを32bits×4で使っても2倍ちょっとしか速くならないわけで、倍精度だとAVX-256以降でないと意味がないからでしょうか。

なお、C++のテンプレート・ライブラリEigenは行列演算などにSIMD拡張命令セットを使ってくれるので、こういう苦しい記述をしないで浮動小数点演算で速度を出したい人はC++/Eigenを使うべきです。CPUのサポートしている命令セットごとにコードを書き換えないといけないって、手間隙な上に混乱してきますからね。

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <emmintrin.h>
#include <time.h>
#include <cpuid.h>

float  x87_sum(float *X, int n){
float s = 0.0;
for (size_t i = 0; i < n; ++i) {
s += X[i];
}
return s;
}

float  simd_sum(float *X, int n){
  static int ws = sizeof(__m128)/sizeof(float);
  __m128  r128, s128 = {0};
float s = 0.0, sws[ws];
  int m = m % ws;

// add by ws-float from [0 n-m]
for (size_t i = 0; i < n - m; i+=ws) {
r128 = _mm_load_ps(&X[i]);
    s128 = _mm_add_ps(r128, s128);
}
// store result of the above code.
  _mm_store_ps(sws, s128);

// sum sws up, and record it into s.
for (size_t i = 0; i < ws; i++) {
    s += sws[i];
  }

// add the rest, [n-m+1 n-1], by a float.
for (size_t i = 1; i <= m; i++) {
    s += X[n - i];
  }

return s;
}

int main(){
  float *X;
  int  n = 10000;
  int i;
  long et;
  int  ws;
  double r1, r2;
  union cpuid_sig {
    unsigned int  i;
    unsigned char  c[4];
  } sig;
  unsigned int highest, eax, ebx, ecx, edx;

  highest = __get_cpuid_max(0x8000000, &sig.i);
  if(0 < __get_cpuid(highest, &eax, &ebx, &ecx, &edx) && 0 != bit_SSE2 & edx){
    printf("SSE2 is supported.\n");
  } else {
    fprintf(stderr, "SSE2 is NOT supported!\n");
    exit(-1);
  }

  ws = sizeof(__m128)/sizeof(float);
  printf("sizeof(__m128)/sizeof(float) = %ld/%ld = %d (%ld)\n", sizeof(__m128), sizeof(float), ws, sizeof(__m128) - sizeof(float)*ws);

// setup X
  X = calloc(n, sizeof(float));
  for(i=0; i<n; i++){
    X[n] = sinf(0.314F*i);
  }

  et = clock();
  r1 = x87_sum(X, n);
  printf("elapsed time of x87 sum: %f\n", (double)(clock() - et)/CLOCKS_PER_SEC);

  et = clock();
  r2 = simd_sum(X, n);
  printf("elapsed time of SSE2 sum: %f\n", (double)(clock() - et)/CLOCKS_PER_SEC);

  printf("the difference of results: %f\n", fabs(r1 - r2));

  return 0;
}

RでべたべたとBHHH法

Berndt-Hall-Hall-Hausmanアルゴリズムは、化石的な最適化アルゴリズムで、実証分析を行っている経済学徒でお世話になったことがある人は、そこそこいると思います。TSPと呼ばれる統計解析パッケージ*1では標準的に使えたのですが、RではmaxLikパッケージ*2などを入れる必要があります。利用困難と言うわけではないですが、人気ではなさそうです。マルコフ連鎖モンテカルロ法が当たり前の時代、古の技法になりつつあると言えるでしょう。しかし、ちょっとした都合でBHHH法の計算手順を確認したいと思います。

1. BHHH法の概要

目的関数として対数尤度関数が与えられたときのことを考えましょう。は被説明変数のベクトル、はパラメーターです*3。もっとも基本的なものはニュートン・ラフソン法になります。真の係数を、推定量を（は反復回数で指数ではない）とすると、

になります。ここで、二階微分の計算があると上手く計算されないことが多々あるので、一階微分しかないフィッシャー情報行列の符号を反転させたもので代用しようと言うのが、BHHHアルゴリズムです。原理上、最尤法の計算ぐらいにしか使えません。

2. データセット

サンプルサイズ10のデータセットです。

X <- t(matrix(c(1, 5.75095, 7.13628, 1, 8.12624, 3.43466, 1, 0.470068, 8.32101, 1, 6.97381, 8.56067, 1, 3.01102, 1.86405, 1, 2.73131, 9.86068, 1, 0.639832, 7.30122, 1, 2.02848, 3.03172, 1, 2.27631, 0.179666, 1, 2.59997, 7.71923), 3))
y <- t(matrix(c(-8.67053, 6.59171, -21.7837, -10.9077, 1.78061, -23.3735, -21.2741, -3.17336, 4.87379, -16.6442), 1))

3. 対数尤度関数とグラディエント

正規分布を仮定した線形回帰を最尤法で求めます。対数尤度関数を一階微分したグラディエントは、フィッシャー情報行列の計算のために、説明変数と従属変数を一つづつ取れるようにします。

# 対数尤度関数
objf <- function(p){
  theta <- p[1]
  len <- length(p)
  b <- matrix(p[2:len], len-1, 1)
  s <- sum((y - X %*% b)^2)
  n <- length(y)
  -n*log(theta^2)/2 - s/theta^2/2
}

# グラディエント
objg <- function(p, y=get("y"), X=get("X")){
  n <- length(y)
  theta <- p[1]
  len <- length(p)
  b <- matrix(p[2:len], len - 1, 1)
  res <- y - X %*% b
  dtheta <- -1*n/theta + sum(res^2)/theta^3
  dbeta <- numeric(length(b))
  for(i in 1:length(b)){
    dbeta[i] <- sum(X[, i]*2*res)/theta^2/2
  }
  c(dtheta, dbeta)
}

4. フィッシャー情報行列の計算

フィッシャー情報行列の計算にヘッシアンが要りそうな感じがする*4のですが、行列がとなる分散共分散行列なので素朴に計算できます。これを観測数で割ったもの*5に-1を乗じて、ヘッシアンの代わりにします。

FIM <- function(p){
  m <- matrix(0, length(y), length(p))
  for(i in 1:length(y)){
    m[i, ] <- objg(p, y[i], matrix(X[i, ], 1))
  }
  (t(m) %*% m)/nrow(m)
}

なお、サンプルサイズを増やすと各セルの値が小さくなりすぎて「システムは数値的に特異です: 条件数の逆数 = ･･･」とエラーが出たりするので、実用的に使うには、もっと改良が要ります。

5. ステップ幅の計算

ステップ幅の具体的な計算方法については原論文やアルゴリズム紹介には言及が無いので、「Rで黄金分割探索」で定義した関数を流用します。BFGS法の実装でも、ステップ幅の計算はまちまちのようで、プログラマに任されているのでしょう。

6. BHHH法による推定

ニュートン・ラフソン法とほとんど一緒です。

init <- c(1, 1, 1, 1) # 初期値
param <- init # 更新していくパラメーターの変数
pv <- objf(param) # 初期値の目的関数の値を保存

for(i in 1:300){ # 収束が遅いので繰り返し回数上限は長めに
  g <- matrix(objg(param, y, X), length(param))
  R <- -1*( FIM(param) / nrow(X) )
#
# 以下に置き換えるとニュートン・ラフソン法になる
#  library("numDeriv")
#  R <- jacobian(function(p){ objg(p, y, X) }, param)
#
  # ステップ幅を計算
  a <- gss(function(a){
    # solve(R) %*% g = solve(R, g)
    objf(param - a * solve(R, g))
  }, min=0, max=1, maximize=TRUE) # データセットを変えてみて、うまく収束しなくなった場合はmin=-1にすると･･･

  # パラメーターを更新
  param <- param - a * solve(R, g)

  # 新たなパラメーターで目的関数の値を計算
  v <- objf(param)

  # 改善幅が小さければ終了
  if(abs(pv - v) < 1e-12){
    print(sprintf("pv - v = %f", pv - v))
    break;
  }

  # 計算の途中経過をばらばらと表示
  print(sprintf("i:%d a=%f", i, a))
  print(round(c(param), 6))

  # 現在のパラメーターの目的関数の値を保存
  pv <- v
}

# 推定結果をリストにまとめる
r_bhhh <- list(
  param = param,
  g = matrix(objg(param, y, X), length(param)),
  R = -1*( FIM(param)/ nrow(X) ) ,
  vcov = -1*solve( FIM(param))
)

7. 推定結果の比較

係数はほぼ同じモノになります。

r_nlm <- nlm(function(p){ -1*objf(p) }, init, hessian=TRUE)
r_ols <- lm(y ~ 0 + X)
r <- matrix(c(r_bhhh$param, r_nlm$estimate, NA, coef(r_ols)), ncol(X) + 1)
colnames(r) <- c("BHHH", "nlm/DSM", "lm/OLS")
r

分散共分散行列は･･･もっとサンプルサイズが要るのでしょう。

*1: ライブラリと言う意味ではなく、箱詰めで売られていると言う意味。

*2: 商用ソフトと言う意味ではなく、ライブラリと言う意味。

*3: パラメーターには分散などが含まれるので、の方が良かったかもです。

*4:教科書に数式の展開で出てくるわけですが、直接計算する練習をさせるものは（たまたまかも知れませんが）見た記憶が無いです。

*5:誤植みたいな部分もあって自信がないのですが、原論文ではそうなっているように読めました。