感染症の罹患経験など、無作為抽出のyes/noの観測値は二項分布に従うことが知られていますが、その場合も正規分布を用いて区間推定を行うことが多いです*1。中心極限定理で正規分布に漸近することを利用しているのですが、稀にしか観測されない事象で、全体の生起数が10にも満たない場合は不適切な推定になりがちです。区間の片方の端がマイナスになります。
例えば厚生労働省の新型コロナウイルスへの抗体保有率の調査の場合、東京都で観測数が1971名、抗体保有者が2名となり、正規分布から区間推定を行うと0.0010(95%信頼区間-0.00039~0.0024)と言う結果になります。2項分布の生起確率でマイナスはあり得ないので、これはちょっとまずいです。プラスの区間になるように、計算精度を上げましょう。
Wilson score intervalを使う
これが無難です。Rのbinomパッケージでサポートされています。
if(!any(suppressWarnings(library(quietly=TRUE, verbose=FALSE)$results[,"Package"] == "binom"))){ stop("Do install.packages(\"binom\") before runnning this script.") } library(binom) binom.confint(2, 1971, conf.level=0.95, methods="wilson")

シミュレーションによる信頼区間の推定
厳密な定義はややこしい信頼区間ですが、帰無仮説でパラメーターの真の値としても、統計的仮説検定で帰無仮説が棄却されないことになる値の区間になります。パラメーターから乱数でデータを生成すると、その上下の裾野が棄却域になるわけですが、裾野ギリギリのところに観測値が来るパラメーターが、信頼区間の境界点となるので、愚直に計算することも可能です。
obs <- 1971 occ <- 2 p <- occ/obs n <- 1000 a <- 0.05 seed <- 849 # 真のパラメーターがqのときの両側a%の棄却域を求める outskirt <- function(q){ set.seed(seed) x <- rbinom(n, obs, q) estimated <- numeric(obs + 1) th0 <- 0 th1 <- obs s <- 0 for(i in 0:obs){ estimated[i + 1] <- sum(x==i) s <- s + estimated[i + 1] if(s < n*a/2){ th0 <- i + 1 } else if(th1==obs && s >= n*(1-a/2)){ th1 <- i } } c(th0/obs, th1/obs) # qbicomを使って出した値で区間を求めると、なぜかbinom.testのP値がa/2ギリギリの値にならない # c(qbinom(a/2, obs, q), qbinom(1-a/2, obs, q))/obs } r_th0 <- optimize(function(q){ abs(p - outskirt(q)[2]) }, c(0, p), tol=1e-12) r_th1 <- optimize(function(q){ abs(outskirt(q)[1] - p) }, c(p, min(1, 5*p)), tol=1e-12) cat(sprintf("%.0f%% CI (%.6f, %.6f)\n", 100*(1-a), r_th0$minimum, r_th1$minimum))
CI (0.000148, 0.003340)とWilson score intervalやClopper and Peason intervalと比較して広めになり、この両端の値を帰無仮説に観測値でbinom.testで統計的仮説検定をかけても棄却にはならないです。棄却域ギリギリのところまでにしているので注意してください。
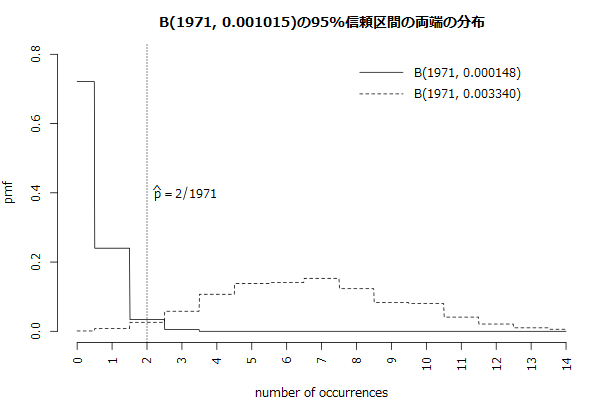
図を描くとB(1971, 0.000148)の右側の裾野の境界、B(1971, 0.003340)の左側の裾野の境界に、観測数2が来ていることが分かります。B(1971, 0.000388)の0から2までの確率質量の合計は0.975以上、B(1971, 0.003340)の2から1971までの確率質量の合計も0.975以上となります。
等裾事後信用区間
ベイズの定理を使って、事前分布と尤度関数の積を1に正規化して事後確率を求める方法で、信頼区間を計算するための確率分布をつくります*2。生起確率を求めるときの2項分布の尤度関数は、観測数と生起数を固定した2項分布の確率密度関数となることに注意すると、計算機にやらせる分にはそんなに難しくない作業になります。
n <- 1971 # 観測数 m <- 2 # 生起数 p <- m/n # 生起確率 v <- n*p*(1-p) # 観測数の分散 prior <- function(p){ # Beta(1/2, 1/2)分布を事前分布に置くとJeffreys intervalという立派な名前になる # dbeta(p, 1/2, 1/2) # 1を置いておくと、事前分布は一様分布[0 1]になる 1 } # 正規化するための尤度関数の積分値 s <- integrate(function(p){ # pを求めるときの2項分布の尤度関数は、観測数と生起数を固定した2項分布の確率密度関数となる dbinom(m, n, p)*prior(p) }, 0, 1, rel.tol=1e-15)$value # 確率密度関数 pdf <- function(p){ r <- numeric(length(p)) for(i in 1:length(p)){ # 事前分布にBeta(1/2, 1/2)を置いていることに注意 r[i] <- dbinom(m, n, p[i])*prior(p[i])/s } r } # 累積分布関数 cdf <- function(ps){ sapply(ps, function(p){ integrate(function(a){ pdf(a) }, 0, p)$value }) } # 閾値(2分探索で計算) threshold <- function(a){ l <- 0 h <- 1 m <- 0.5 for(i in 1:100){ m <- (l + h)/2 v <- cdf(m) - a if(v == 0){ break; } else if(v < 0){ l <- m } else { h <- m } } m } # 95%信頼区間とする a <- 0.025 sprintf("%.4f(%.0f%%信頼区間%.5f~%.5f)", p, 100*(1-2*a), threshold(a), threshold(1-a))
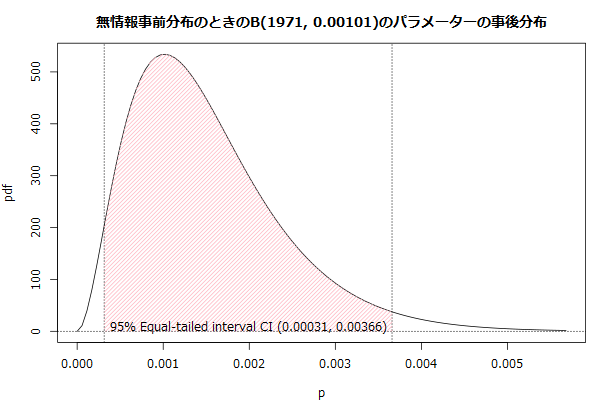
0.0010(95%信頼区間0.00031~0.00366)と計算できました。なお、正規分布からの区間推定は以下で計算できるので、mが50ぐらいのときはほぼ変化なしな事を確認すると、安心して使いやすいと思います。
se <- sqrt(v)/n # 生起確率の標準誤差 rng <- se*qnorm(a, lower.tail=FALSE) sprintf("%.4f(%.0f%%信頼区間%.5f~%.5f)", p, 100*(1-2*a), p - rng, p + rng)
最高事後密度信用区間
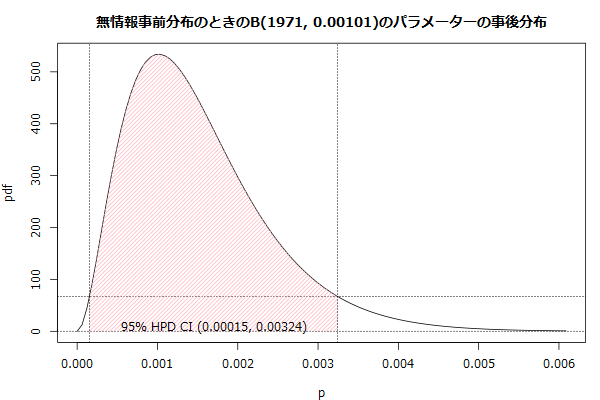
最高事後密度信用区間(HPD: highest posterior density)で計算しろって言われたので追記。広く使われている両側の裾野の面積が同じになる信頼区間の代わりにしたら混乱がありそうですが。
n <- 1971 # 観測数 m <- 2 # 生起数 p <- m/n # 生起確率 v <- n*p*(1-p) # 観測数の分散 # 正規化するための尤度関数の積分値 s <- integrate(function(p){ # pを求めるときの2項分布の尤度関数は、観測数と生起数を固定した2項分布の確率密度関数となる dbinom(m, n, p) }, 0, 1, rel.tol=1e-15)$value # 確率密度関数 ppdf <- function(p){ r <- numeric(length(p)) for(i in 1:length(p)){ r[i] <- dbinom(m, n, p[i])/s } r } # 累積分布関数 # minpdf <= pdf(x)のpdf(x)の値だけ積分する cdf <- function(minpdf){ integrate(function(a){ v <- ppdf(a) ifelse(minpdf <=v, v, 0) }, 0, 1)$value } # Highest Posterior Densityで95%信用区間のpdfの閾値を求める # pdf(x)が一定以上のxの点だけHPDの領域に入る a <- 0.025 r_optimize <- optimize(function(minpdf){ abs(cdf(minpdf) - (1 - 2*a)) }, c(0, ppdf(p))) mpdf <- r_optimize$minimum # Highest Posterior Densityは多峰に対応するというか、区間が分割される可能性がある # chgpの奇数アドレスに開始点を、偶数アドレスに終了点を詰んでいく xlim <- c(0, 6*p) chgp <- numeric() x <- seq(xlim[1], xlim[2], length.out=100) # プロットのピンク部が粗い場合はグリッドサイズを増やす y <- ppdf(x) flag <- FALSE for(i in 1:length(x)){ if(flag){ if(y[i] <= mpdf){ flag <- FALSE chgp <- c(chgp, i) # グリッドから計算すると低精度なので、境界値を高精度に求める if(1<i){ r_optimize <- optimize(function(p){ abs(mpdf - ppdf(p)) }, c(x[i-1], x[i]), tol=1e-12) # x[i]とy[i]を更新 x[i] <- r_optimize$minimum y[i] <- ppdf(x[i]) } } } else { if(y[i] >= mpdf){ flag <- TRUE chgp <- c(chgp, i) # グリッドから計算すると低精度なので、境界値を高精度に求める if(1<i){ r_optimize <- optimize(function(p){ abs(mpdf - ppdf(p)) }, c(x[i-1], x[i]), tol=1e-12) # x[i]とy[i]を更新 x[i] <- r_optimize$minimum y[i] <- ppdf(x[i]) } } } } j <- 1 while(j < length(chgp)){ th0 <- x[chgp[j]] th1 <- x[chgp[j + 1]] cat(sprintf("%.0f%% HPD CI (%.5f, %.5f)\n", 100*(1-2*a), th0, th1)) j <- j + 2 }